23ος ΠΔΠ Καμπ (seniors)
Βελτίωση οδικού δικτύου (newroad)

Σε μια χώρα υπάρχουν \(N\) πόλεις και \(M\) δρόμοι που συνδέουν μεταξύ τους κάποιες από αυτές τις πόλεις. Θεωρούμε ότι οι δρόμοι είναι κατευθυνόμενοι και ότι ο δρόμος που πηγαίνει από την πόλη \(u\) στην πόλη \(v\) έχει (μη αρνητικό) μήκος \(L(u, v)\).

Πρόκειται να κατασκευαστεί ένας νέος δρόμος και έχει προταθεί μία λίστα \(K\) ζευγών πόλεων που θα μπορούσε αυτός ο δρόμος να συνδέσει. Κάθε προτεινόμενος δρόμος από την πόλη \(u\) στην πόλη \(v\) συνοδεύεται από το αντίστοιχο μήκος του \(L(u, v)\).

Έστω δύο δεδομένες πόλεις, \(s\) και \(t\). Το ζητούμενο είναι να επιλέξουμε το προτεινόμενο δρόμο που επιτυγχάνει την μέγιστη μείωση της απόστασης από την πόλη \(s\) στην πόλη \(t\).

Αρχεία Εισόδου (newroad.in):

Η πρώτη γραμμή της εισόδου περιέχει πέντε φυσικούς αριθμούς, χωρισμένους ανά δύο με ένα κενό διάστημα: το πλήθος \(N\) των πόλεων, το πλήθος \(M\) των δρόμων, το πλήθος \(K\) των προτεινόμενων δρόμων, τον αριθμό \(s\) της πόλης αφετηρίας και το αριθμό \(t\) της πόλης τερματισμού. Κάθε μία από τις επόμενες \(M\) γραμμές περιγράφει έναν δρόμο και περιέχει τρεις φυσικούς αριθμούς \(u\), \(v\), \(L\), χωρισμένους ανά δύο με ένα κενό διάστημα: την πόλη \(u\) απ’ όπου ξεκινά ο δρόμος, την πόλη \(v\) στην οποία καταλήγει, και το μήκος του \(L\). Κάθε μία από τις επόμενες \(K\) γραμμές περιγράφει έναν προτεινόμενο δρόμο και περιέχει πάλι τρεις φυσικούς αριθμούς \(u\), \(v\), \(L\), όπως και προηγουμένως.

Η αρίθμηση των πόλεων, των δρόμων, και των προτεινόμενων δρόμων γίνεται σε αύξουσα σειρά ξεκινώντας από το \(1\).

Αρχεία Εξόδου (newroad.out):

Η έξοδος πρέπει να αποτελείται από μία γραμμή που να περιέχει ακριβώς έναν ακέραιο αριθμό: την ελάχιστη απόσταση από την πόλη \(s\) στην πόλη \(t\) που επιτυγχάνεται όταν επιλεγεί ο καλύτερος δυνατός προτεινόμενος δρόμος.

Προσέξτε ότι είναι πιθανό κανένας από τους προτεινόμενους δρόμους να μην επιφέρει μείωση της απόστασης από την πόλη \(s\) στην πόλη \(t\). Σε αυτήν την περίπτωση, δε χρειάζεται να επιλέγεται κανένας από τους προτεινόμενους δρόμους και το αποτέλεσμα πρέπει να είναι η απόσταση μεταξύ \(s\) και \(t\), όπως είναι στο ήδη υπάρχον οδικό δίκτυο.

Παράδειγμα Αρχείου Εισόδου - Εξόδου:

newroad.in	newroad.out
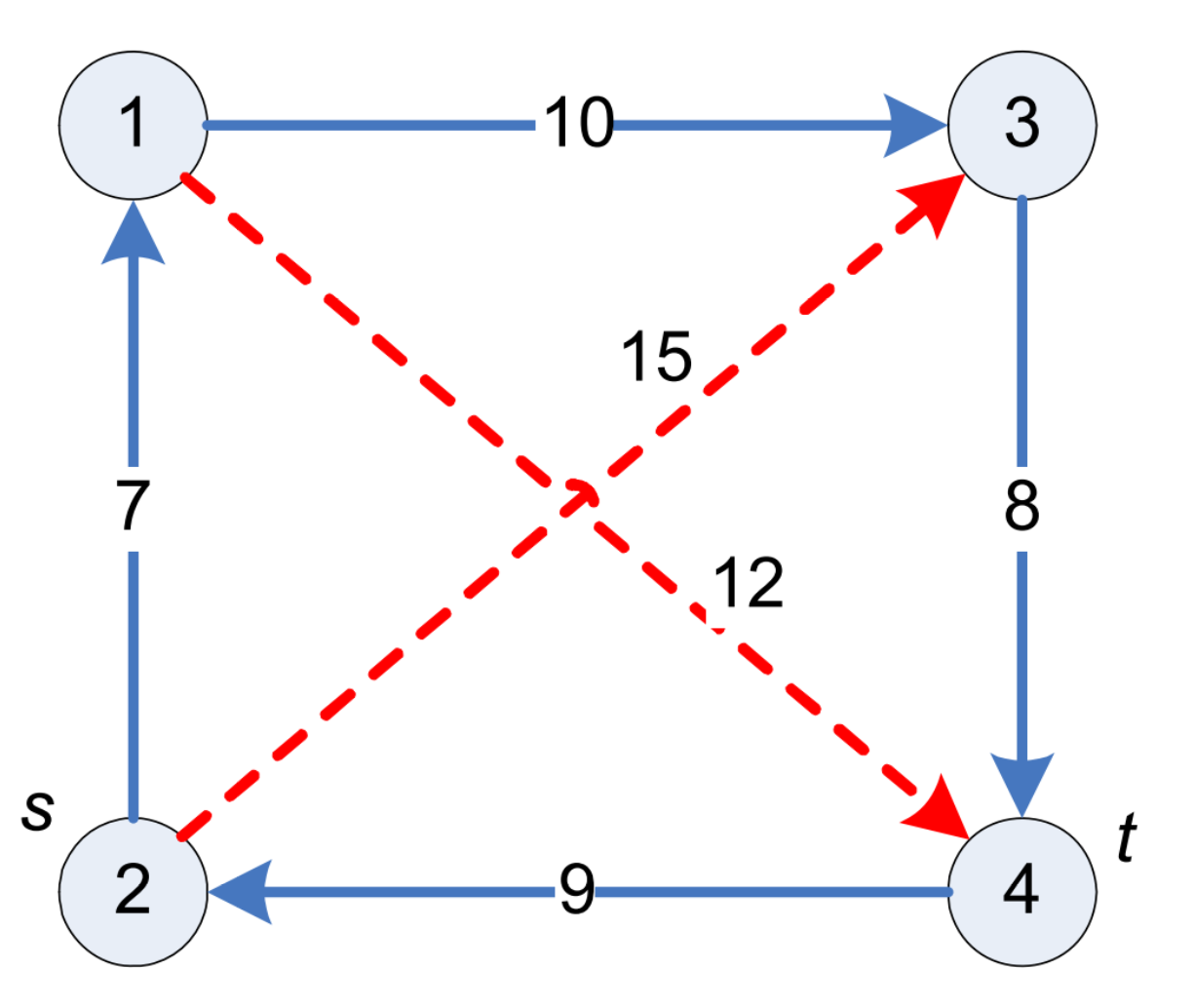
4 4 2 2 4 1 3 10 2 1 7 4 2 9 3 4 8 2 3 15 1 4 12	19

Περιορισμοί:

• \(2 \leq N \leq 10.000\), \(1 \leq M \leq 100.000\), \(1 \leq K \leq 10.000\).
• Κάθε διαδρομή που δεν περιέχει κύκλο έχει μήκος το πολύ \(2.000.000.000\).
• Όριο χρόνου εκτέλεσης: \(1\) sec.
• Όριο μνήμης: \(128\) MB.