24ος ΠΔΠ B' Φάση: Ραδιοαστέρες (pulsars) - Λύση
Επεξήγηση προβλήματος
Όπως αναφέρει και η εκφώνηση, το συγκεκριμένο πρόβλημα είναι μια εφαρμογή του υπολογισμού του ελάχιστου κυρτού πολυγώνου (convex hull) των σημείων που δίνονται. Μπορείτε να διαβάσετε περισσότερες πληροφορίες στη Βικιπαίδεια για τον ορισμό και τις ιδιότητες του καθώς και για διάφορους αλγορίθμους που χρησιμοποιούνται για την εύρεσή του.
Για να κατανοήσουμε πιο εύκολα το ζητούμενο του προβλήματος, μπορούμε να φανταστούμε ότι τα σημεία μας είναι ακίνητα στο χώρο (π.χ. καρφωμένες πινέζες ή καρφιά) και προσπαθούμε να τυλίξουμε μιά ελαστική κορδέλα γύρω τους. Το τελικό σχήμα της κορδέλας θα είναι το ελάχιστο κυρτό πολύγωνο. Στην παρακάτω εικόνα ο εξωτερικός κύκλος δείχνει την ελαστική κορδέλα στην αρχική της θέση πριν την αφήσουμε και το μπλε πολύγωνο το τελικό σχήμα της κορδέλας γύρω από τα σημεία μας.
Αλγόριθμος gift wrapping (\(\mathcal{O}(N^2)\))
Σημείωση: Κανονικά σύμφωνα με τους γραπτούς περιορισμούς και όρια στην εκφώνηση αυτή η λύση δεν θα έπρεπε να περνάει όλα τα testcases. Λόγω όμως των αδύναμων testcases περνάει.
Μια άλλη προσέγγιση του προβλήματος είναι να σκεφτούμε ότι τυλίγουμε τα σημεία μας με ένα χαρτί περιτυλίγματος, όπως θα κάναμε με ένα δώρο.
Ξεκινάμε με ένα σημείο που είναι σίγουρα στο ελάχιστο κυρτό πολύγωνο, π.χ. το πιο αριστερό (και το πιο πάνω σε περίπτωση ισοβαθμίας) σημείο.
Έπειτα, διαλέγουμε το δεύτερο σημείο, έτσι ώστε όλα τα υπόλοιπα σημεία να είναι δεξιά (ή αριστερά αρκεί να διατηρήσουμε την ίδια σύμβαση στη συνέχεια) από τη γραμμή που ενώνει αυτό το σημείο με το πρώτο.
Σε περίπτωση συνευθειακών σημείων, μπορούμε να διαλέγουμε το πιο μακρινό ή το πιο κοντινό ανάλογα με τις ανάγκες μας, παρ’ όλα αυτά στο συγκεκριμένο πρόβλημα η εκφώνηση μας διαβεβαιώνει ότι δεν υπάρχουν τρία ή περισσότερα συνευθειακά σημεία πάνω στο τελικό πολύγωνο.
Με την ίδια λογική επιλέγουμε το τρίτο σημείο έτσι ώστε όλα τα σημεία να είναι δεξιά από τη γραμμή που ενώνει το δεύτερο με το τρίτο σημείο, και ούτω καθεξής. Όταν το επόμενο σημείο που βάζουμε είναι το πρώτο τότε ο αλγόριθμος τελειώνει.

Για να βρούμε το αρχικό σημείο, πρέπει να βρούμε το σημείο με την ελάχιστη τετμημένη (\(x\)), το οποίο μπορούμε να το υπολογίσουμε με ένα πέρασμα από όλα τα σημεία σε χρόνο \(\mathcal{O}(N)\).
Για κάθε επόμενο σημείο, πρέπει να περάσουμε από όλα τα σημεία ώστε να βρούμε αυτό του οποίου η ευθεία αφήνει τα υπόλοιπα σημεία στα δεξιά. Για να το βρούμε αυτό μπορούμε είτε να υπολογίσουμε την κλίση της ευθείας και έπειτα την γωνία της με τον άξονα \(x\) είτε να χρησιμοποιήσουμε το εξωτερικό γινόμενο (πιο συγκεκριμένα την \(z\) συντεταγμένη του). Γενικά στον προγραμματισμό για αυτή τη χρήση, χρησιμοποιούμε το εξωτερικό γινόμενο για λόγους ταχύτητας, ακρίβειας και ευκολίας γραψίματος. Η συνάρτηση υπολογισμού του εξωτερικού γινομένου, μπορεί να γραφτεί έτσι:
long long ccw(Point A, Point B, Point C)
{
return (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y);
}
Αν το αποτέλεσμα της συνάρτησης είναι \(>0\) τότε το σημείο \(\rm C\) είναι αριστερά της ευθείας \(\overline{\rm AB}\), αν είναι \(<0\), είναι δεξιά και αν είναι \(=0\), τότε τα σημεία είναι συνευθειακά.
Αφού ο υπολογισμός του εξωτερικού γινομένου είναι \(\mathcal{O}(1)\) (μόνο πολλαπλασιασμοί και προσθέσεις), ο συνολικός χρόνος περάσματος όλων των σημείων είναι \(\mathcal{O}(N)\). Πρέπει να επαναλάβουμε την διαδικασία για όλα τα σημεία του ελάχιστου κυρτού πολυγώνου, τα οποία μπορεί να είναι έως και \(\mathcal{O}(N)\) αν όλα τα σημεία είναι πάνω στο πολύγωνο.
Πιο συγκεκριμένα, αν το ελάχιστο κυρτό πολύγωνο έχει \(H\) σημεία, τότε μπορούμε να γράψουμε την πολυπλοκότητα ώς \(\mathcal{O}(NH)\). Σε περίπτωση που του \(H\) είναι σημαντικά μικρότερο από το \(N\), τότε ο αλγόριθμος μπορεί να τρέξει πολύ γρήγορα σχετικά με την αρχική πολυπλοκότητα \(\mathcal{O}(N^2)\). Αυτός είναι ο λόγως που τα αρχεία ελέγχου του συγκεκριμένου προβλήματος είναι σχετικά αδύναμα, καθώς οι λύσεις έχουν πολύ λίγα σημεία σε σχέση με το \(N\).
Χρειάζεται, επιπλέον στο τέλος μία ταξινόμηση με βάση την σειρά που είχαν στο αρχείο εισόδου, όπως ζητάει η εκφώνηση. Η πολυπλοκότητα της ταξινόμησης είναι \(\mathcal{O}(N\log N)\) άμα χρησιμοποιήσουμε μια συνάρτηση ταξινόμησης όπως η quicksort για παράδειγμα.
Άρα η συνολική πολυπλοκότητα είναι \(\mathcal{O}(N\cdot N + N + N\log N) = \mathcal{O}(N^2)\).
int main()
{
FILE *fin = fopen("pulsars.in", "r");
FILE *fout = fopen("pulsars.out", "w");
fscanf(fin, "%d", &N);
// Διαβάζουμε τα δεδομένα εισόδου και βρίσκουμε το πιο αριστερό (και το πιο
// κάτω σημείο), το οποίο είναι πάντα μέρος της λύσης.
int startPoint = 0;
for (int i = 0; i < N; ++i)
{
inHull[i] = false;
fscanf(fin, "%lld %lld", &points[i].x, &points[i].y);
if (points[i] < points[startPoint])
startPoint = i;
}
fclose(fin);
points.resize(N);
// Ξεκινάμε από το αρχικό (ελάχιστο) σημείο.
inHull[startPoint] = true;
int currentPoint = startPoint;
int totalHullPoints = 1;
// Επαναλαμβάνουμε μέχρι να ξαναβρούμε το αρχικό (ελάχιστο) σημείο.
while (true)
{
// Ελέγχουμε πάντα το startPoint εκτός από την πρώτη επανάληψη για να
// ξέρουμε πότε να σταματήσουμε (όταν το startPoint ειναι το nextPoint στο
// τέλος της επανάληψης).
int nextPoint = startPoint;
if (currentPoint == startPoint)
nextPoint = -1;
// Περνάμε όλα τα σημεία για να βρουμε πιο είναι το πιο δεξια ως προς το
// currentPoint.
for (int i = 0; i < N; ++i)
{
// Προσπερνάμε όλα τα σημεία που είναι ήδη στο πολύγωνο.
if (inHull[i])
continue;
// Αναθέτουμε μια τιμή σε περίπτωση που δεν το κάναμε πριν.
if (nextPoint == -1)
{
nextPoint = i;
continue;
}
// Ελέγχουμε αν το σημείο i είναι πιο δεξιά από το nextPoint
// και αν ειναι, ανανεώνουμε την τιμή του.
if (ccw(points[currentPoint], points[nextPoint], points[i]) < 0)
nextPoint = i;
}
// Σταματάμε αν γυρίσαμε στην αρχή.
if (nextPoint == startPoint)
{
break;
}
// Βρήκαμε κι άλλο σημείο της λύσης, οπότε συνεχίζουμε.
currentPoint = nextPoint;
inHull[currentPoint] = true;
totalHullPoints++;
}
fprintf(fout, "%d\n", totalHullPoints);
for (int i = 0; i < N; ++i)
{
if (inHull[i])
{
fprintf(fout, "%d\n", i + 1);
}
}
fclose(fout);
}
Δείτε ολόκληρη την υλοποίηση εδώ.
Αλγόριθμος Graham scan \(\mathcal{O}(N\log N)\)
Μια άλλη λύση με καλύτερη πολυπλοκότητα είναι ο αλγόριθμος του Graham Scan.
Ο αλγόριθμός ξεκινάει όπως και το gift wrapping βρισκοντας ένα σημείο που είναι σίγουρα στο ελάχιστο κυρτό πολύγωνο, οπότε θα πάρουμε το πιο αριστερά σημείο στο δικό μας παράδειγμα, ας το ονομάσουμε \(\rm P_0\). Έπειτα, ταξινομεί τα σημεία ως προς τη γωνία που σχηματίζει η ευθεία που τα ενώνει με το σημείο \(\rm P_0\) και ο άξονας \(x\). Δεν χρειάζεται να υπολογίσουμε την ακριβή γωνία για να τα ταξινομήσουμε, οποιαδήποτε συνάρτηση που παρουσιάζει αυστηρή μονοτονία στο διάστημα \([-\frac{\pi}{2}, \frac{\pi}{2}]\), όπως π.χ. η κλίση της ευθείας (με προσοχή στις κατακόρυφες ευθείες με άπειρη κλίση). Στο συγκεκριμένο παράδειγμα, θα χρησιμοποιήσουμε το εξωτερικό γινόμενο που αναφέραμε παραπάνω, το οποίο μας γλιτώνει από μερικά edge cases. Χρησιμοποιώντας το σαν το comparison function μπορούμε να ταξινομήσουμε τα σημεία (βλέπε sort, Compare).
sort(points.begin() + 1, points.end(), [](const Point &a, const Point &b)
{ return ccw(points[0], a, b) > 0; });
Έπειτα δημιουργούμε μία στοίβα η οποία θα κρατάει τα στοιχεία του ελάχιστου κυρτού πολυγώνου, στην οποία αρχικά βάζουμε το σημείο \(\rm P_0\) και το πρώτο σημείο από την ταξινομημένη λίστα. Έπειτα, περνώντας ένα ένα τα σημεία στη ταξινομημένη λίστα κάνουμε τον εξής έλεγχο:
- Αν το σημείο “στρίβει” αριστερά σε σχέση με τα δύο τελευταία σημεία στη στοίβα, τότε το προσθέτουμε στη στοίβα και προχωράμε στο επόμενο σημείο.
- Αν το σημείο “στρίβει” δεξιά σε σχέση με τα δύο τελευταία σημεία στη στοίβα ή είναι συνευθειακό (η τελευταία συνθήκη εξαρτάται από τις απαιτήσεις του προβλήματος), αφαιρούμε το τελευταίο σημείο από τη στοίβα και επαναλαμβάνουμε τον έλεγχο.
Ο έλεγχος για τον αν “στρίβουμε” αριστερά ή δεξιά μπορεί να γίνει και πάλι χρησιμοποιώντας το εξωτερικό γινόμενο.
for (int i = 0; i < points.size(); ++i)
{
while (hull.size() > 1 && ccw(hull[hull.size() - 2], hull[hull.size() - 1], points[i]) <= 0)
hull.pop_back();
hull.push_back(points[i]);
}
Στην παραπάνω εικόνα, το \(\rm PAB\) και \(\rm ABC\) στρίβουν αριστερά, αλλά το \(\rm BCD\) όχι, άρα βγάζουμε το τελευταίο σημείο \(\rm C\) από τη λίστα. Τώρα το \(\rm ABD\) στρίβει αριστερά, οπότε συνεχίζουμε.
Σημείωση: Αν έχουμε ταξινομήσει τα σημεία μας σε φθίνουσα σειρά με βάση τη γωνία τους, τότε το αριστερά και το δεξιά στις παραπάνω 2 οδηγίες αντιστρέφονται.
Όταν περάσουμε από όλα τα σημεία, το ελάχιστο κυρτό πολύγωνο είναι τα σημεία στη στοίβα μας (και με τη σειρά που μπήκανε). Αρκεί στο τέλος μία ταξινόμηση με βάση την σειρά που είχαν στο αρχείο εισόδου, όπως ζητάει η εκφώνηση.
Έπειτα η πολυπλοκότητα της κατασκευής του πολυγώνου είναι \(\mathcal{O}(N)\). Μπορεί να μοιάζει σαν \(\mathcal{O}(N^2)\) αρχικά, καθώς μπορεί να αδειάσουμε ολόκληρη τη στοίβα σε κάποια επανάληψη, η οποία μπορεί να φτάσει ως και \(N\) στοιχεία, αλλά αρκεί να παρατηρήσουμε ότι κάθε στοιχείο μπορεί να μπει μέχρι μια φορά και να βγει μέχρι μία φορα, άρα συνολικά το πολύ 2 πράξεις για κάθε σημείο, κάνοντας την τελική πολυπλοκότητα \(\mathcal{O}(N)\).
Άρα η συνολική πολυπλοκότητα, μαζί με την τελική ταξινόμηση ως προς τη σειρά εμφάνισης των σημείων στο αρχείο εισόδου είναι \(\mathcal{O}(N\log N + N + N\log N) = \mathcal{O}(N\log N)\).
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
typedef long long ll;
const int MAXN = 1e6 + 5;
struct Point
{
ll x, y;
int index;
// Ορίζουμε τον τελεστή < ώστε να μπορούμε να το χρησιμοποιήσουμε με τo struct
// π.χ. pointA < pointB. Πρώτα συγκρίνουμε τις τετμημένες (x) και μετά τις
// τεταγμένες (y). Επίσης, ο τελεστής αυτό με τη συνάρτηση sort, αν δεν
// παρέχουμε custom συνάρτηση ταξινόμησης.
bool operator<(const Point &other)
{
return x < other.x || (!(other.x < x) && y < other.y);
}
};
int N;
vector<Point> points(MAXN);
vector<Point> hull;
// Υπολογίζει την συντεταγμένη z του εξωτερικού γινομένου (b-a) x (c-a).
// Θετικό σημαίνει ότι το c είναι αριστερά του διανύσματος ab.
ll ccw(Point a, Point b, Point c)
{
return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y);
}
int main()
{
FILE *fin = fopen("pulsars.in", "r");
FILE *fout = fopen("pulsars.out", "w");
fscanf(fin, "%d", &N);
for (int i = 0; i < N; ++i)
{
points[i].index = i + 1;
fscanf(fin, "%lld %lld", &points[i].x, &points[i].y);
}
fclose(fin);
points.resize(N);
// Βρίσκουμε το πιο αριστερό (και το πιο κάτω σημείο), το οποίο είναι πάντα
// μέρος της λύσης.
int startPoint = 0;
for (int i = 0; i < points.size(); ++i)
{
if (points[i] < points[startPoint])
startPoint = i;
}
// Μετακινούμε το startPoint στην αρχή της λίστας για να μην το σορτάρουμε
// μαζί με τα υπόλοιπα.
Point tmp = points[0];
points[0] = points[startPoint];
points[startPoint] = tmp;
// Σορτάρουμε ως προς τη γωνία με το αρχικό σημείο.
sort(points.begin() + 1, points.end(), [](const Point &a, const Point &b)
{ return ccw(points[0], a, b) > 0; });
// Αφαιρούμε σημεία από τη στοίβα hull έως ότου το καινούργιο σημείο να
// δημιουργεί αριστερή στροφή.
for (int i = 0; i < points.size(); ++i)
{
while (hull.size() > 1 && ccw(hull[hull.size() - 2], hull[hull.size() - 1], points[i]) <= 0)
hull.pop_back();
hull.push_back(points[i]);
}
fprintf(fout, "%ld\n", hull.size());
// Ταξινομούμε τα σημεία ως προς τη θεση τους στο αρχείο εισόδου.
sort(hull.begin(), hull.end(),
[](const Point &a, const Point &b)
{ return a.index < b.index; });
for (const auto &p : hull)
{
fprintf(fout, "%d\n", p.index);
}
fclose(fout);
}
Αλγόριθμος monotone chain \(\mathcal{O}(N\log N)\)
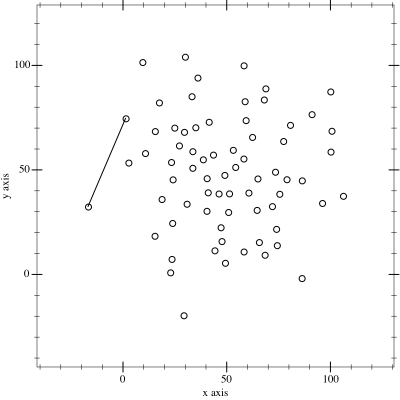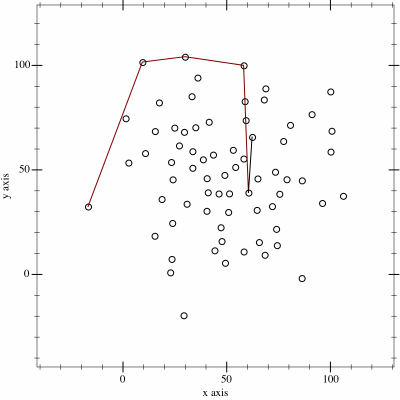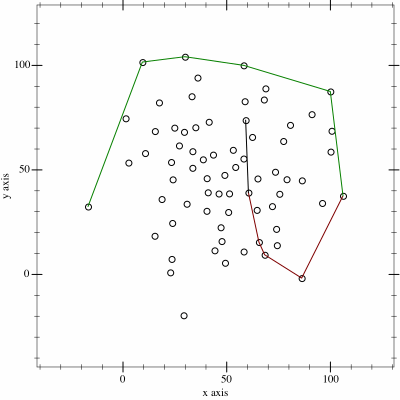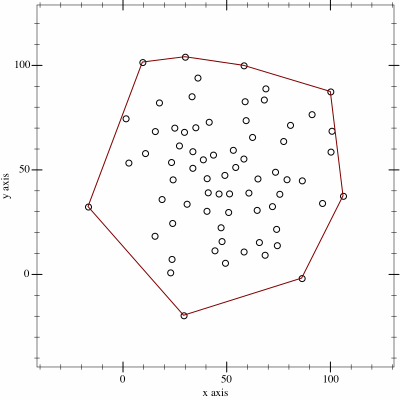
Ο αλγόριθμος αυτός μοιάζει πολύ με τον προηγούμενο, μόνο που το πολύγωνο το φτιάχνουμε σε δύο μισά (άνω και κάτω) τα οποία στο τέλος ενώνουμε. Στην αρχή ταξινομούμε τα σημεία τους με βάση την τετμημένη (\(x\)) (και την τεταγμένη \(y\) σε περίπτωση ισότητας). Έπειτα, εφαρμόζουμε τον παραπάνω αλγόριθμο στην ταξινομημένη λίστα δύο φορές, την πρώτη κρατώντας τις αριστερές στροφές όπως πριν, φτιάχνοντας το κάτω μισό, και την δεύτερη κρατώντας τις δεξιές στροφές, φτιάχνοντας το άνω μισό.
Έπειτα μπορούμε να ενώσουμε τα δύο μισα και να ταξινομήσουμε όπως ζητάει η εκφώνηση.

Η συνολική πολυπλοκότητα είναι όπως και στον Graham Scan, αφού τρέχουμε τον ίδιο αλγόριθμο, απλά δύο φορές και χρησιμοποιώντας διαφορετική ταξινόμηση.
Σε περίπτωση που θέλαμε τη σειρά των σημείων όπως εμφανίζονται στο ελάχιστο κυρτό πολύγωνο, θα μπορούσαμε να αντιστρέψουμε τα σημεία σε ένα από τα δύο μισά και να το προσθέσουμε στο τέλος του άλλου μισού.
Δείτε την υλοποίηση εδώ.