24ος ΠΔΠ Καμπ (seniors)
Αύξουσα πολυγωνική γραμμή (cutpoly)

Δίνεται μία πολυγωνική γραμμή \(N\) σημείων στο επίπεδο. Τα σημεία είναι διατεταγμένα ως προς \(x\), δηλαδή \(x_{i+1} > x_i\) και επίσης η πολυγωνική γραμμή είναι γνησίως αύξουσα ως προς \(y\), δηλαδή \(y_{i+1} > y_i\).

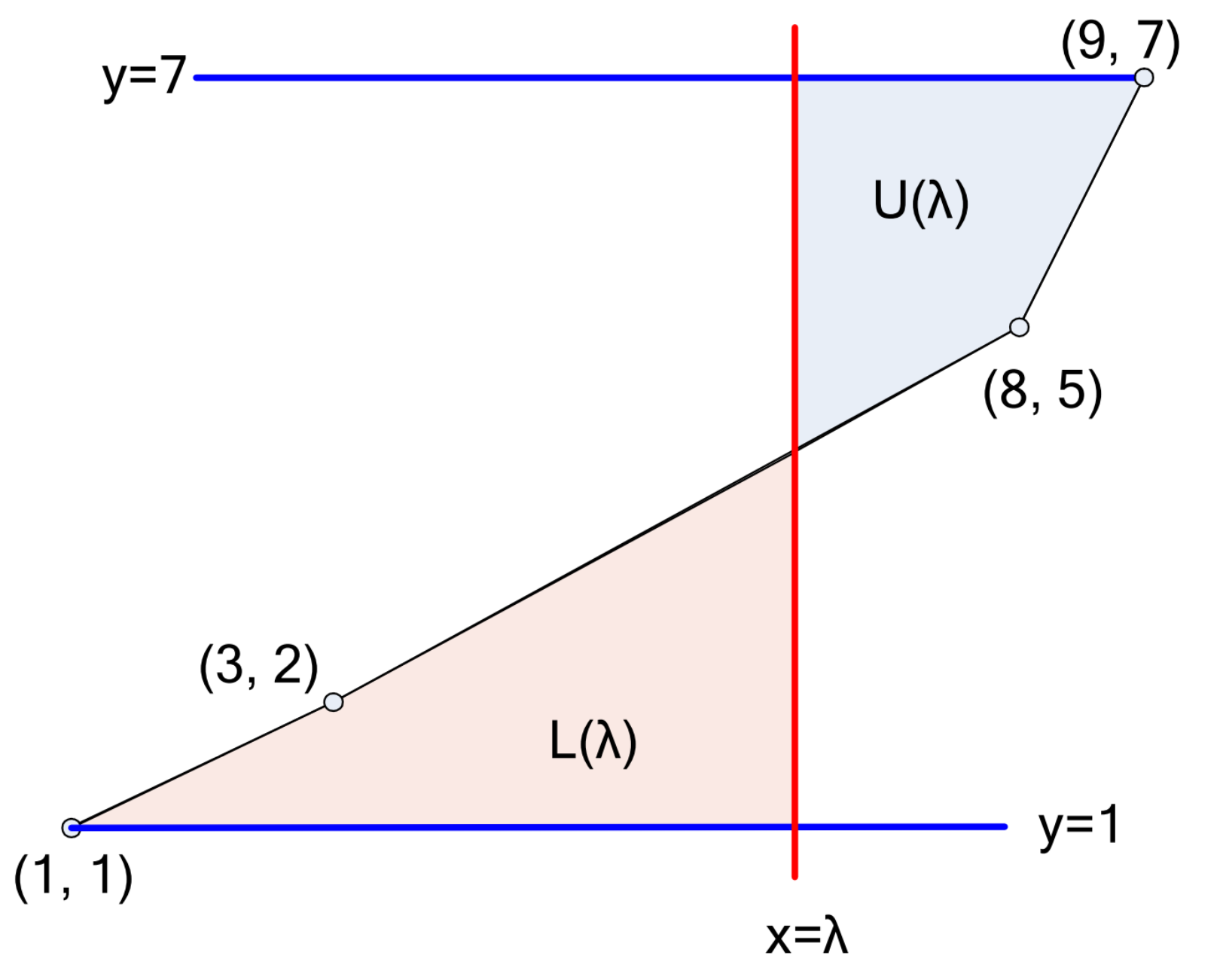
Έστω οι ευθείες \(y = y_1\), και \(y = y_N\), παράλληλες στον άξονα των \(x\). Μπορούμε να φέρουμε μία ευθεία \(x = \lambda\) παράλληλη στον άξονα των \(y\) η οποία τέμνει την πολυγωνική γραμμή σε ένα σημείο (\(x_1 \leq \lambda \leq x_N\)). Μπορεί να την τέμνει σε κάποιο από τα \(N\) σημεία που δίνονται ή μπορεί να τέμνει κάποιο από τα \(N-1\) ευθύγραμμα τμήματα που σχηματίζονται. Έστω \(L(\lambda)\) το εμβαδό που περικλείεται από την πολυγωνική γραμμή, την ευθεία \(y = y_1\) και την ευθεία \(x = \lambda\). Έστω \(U(\lambda)\) το εμβαδό που περικλείεται από την πολυγωνική γραμμή, την ευθεία \(y = y_N\) και την ευθεία \(x = \lambda\).

Ζητείται να προσδιοριστεί η ελάχιστη τιμή του \(L(\lambda) + U(\lambda)\).

Αρχεία Εισόδου (cutpoly.in):

Η πρώτη γραμμή της εισόδου θα περιέχει μόνο τον ακέραιο αριθμό \(N\), το πλήθος των σημείων της πολυγωνικής γραμμής. Κάθε μία από τις επόμενες \(N\) γραμμές περιέχει ένα ζεύγος ακεραίων αριθμών χωρισμένων μεταξύ τους με ένα κενό, που αντιστοιχούν στις συντεταγμένες \(x\) και \(y\) αντίστοιχα καθενός σημείου της γραμμής. Τα σημεία θα δίνονται ταξινομημένα ως προς τη διάσταση \(x\).

Αρχεία Εξόδου (cutpoly.out):

Η έξοδος πρέπει να αποτελείται από έναν πραγματικό αριθμό, την ελάχιστη δυνατή τιμή του \(L(\lambda) + U(\lambda)\), με ακρίβεια \(6\) δεκαδικών ψηφίων. Προσοχή! Τυπώστε με %0.6lf\n ή κάτι αντίστοιχο.

Παράδειγμα Αρχείου Εισόδου - Εξόδου:

1^o

cutpoly.in	cutpoly.out
4 1 1 3 2 8 5 9 7	12.833333

Περιορισμοί:

• \(2 \leq N \leq 1.000.000\).
• Όριο χρόνου εκτέλεσης: \(1\) sec.
• Όριο μνήμης: \(64\) MB.