24ος ΠΔΠ Καμπ (seniors)
Μεταφορά τροφίμων (shades)

Δίνεται ένας χάρτης στον οποίο βρίσκονται σημειωμένες \(N\) πόλεις, που συνδέονται μεταξύ τους με ένα δίκτυο \(M\) δρόμων μονής κατεύθυνσης. Κάποιες πόλεις είναι αγροτικές και σημειώνονται στο χάρτη με άσπρο χρώμα. Κάποιες άλλες πόλεις είναι αστικές και σημειώνονται στο χάρτη με μαύρο χρώμα. Τέλος, οι πόλεις που δεν είναι ούτε αγροτικές ούτε αστικές σημειώνονται στο χάρτη με γκρίζο χρώμα.

Οι αγροτικές πόλεις παράγουν τρόφιμα και οι αστικές τα καταναλώνουν. Είναι επόμενο, λοιπόν, τα τρόφιμα να ταξιδεύουν από τις αγροτικές πόλεις προς τις αστικές, κατά μήκος των δρόμων. Οι πόλεις από τις οποίες περνούν τα τρόφιμα στη διαδρομή τους είναι τυχερές γιατί εκεί η οικονομία ανθίζει.

Συγκεκριμένα, μία πόλη είναι τυχερή αν βρίσκεται πάνω σε κάποια διαδρομή που ξεκινάει από μία αγροτική πόλη (άσπρη), καταλήγει σε μία αστική πόλη (μαύρη) και δεν περιέχει άλλη αστική πόλη εκτός από την τελική (διαφορετικά τα τρόφιμα θα κινδύνευαν να φαγωθούν στο δρόμο και ίσως να μην ταξίδευαν μέχρι το τέλος της διαδρομής). Προσέξτε ότι σε μία τέτοια διαδρομή, τόσο η αρχική αγροτική πόλη όσο και η τελική αστική πόλη θεωρούνται τυχερές. Προσέξτε επίσης ότι μεταξύ της αρχικής αγροτικής πόλης και της τελικής αστικής μπορούν να υπάρχουν και άλλες αγροτικές πόλεις.

Ζητείται να βρείτε ποιες πόλεις είναι τυχερές.

Αρχεία Εισόδου (shades.in):

Η πρώτη γραμμή της εισόδου θα περιέχει δύο ακέραιους αριθμούς \(N\) και \(M\), χωρισμένους με ένα κενό διάστημα: το πλήθος των πόλεων και το πλήθος των δρόμων. Η δεύτερη γραμμή θα περιέχει \(N\) αριθμούς χωρισμένους ανά δύο με ένα κενό διάστημα, οι τιμές των οποίων θα είναι \(0\), \(1\) ή \(2\). Κάθε τέτοια τιμή θα αντιστοιχεί κατά σειρά σε μία πόλη. Αν η τιμή είναι \(0\), η πόλη είναι αγροτική (άσπρη), αν είναι \(1\) τότε η πόλη είναι αστική (μαύρη) και αν είναι \(2\) τότε δεν είναι ούτε αγροτική ούτε αστική (γκρίζα). Κάθε μία από τις επόμενες \(M\) γραμμές θα περιέχει ένα ζεύγος αριθμών \(A\), \(B\), με τιμές μεταξύ \(1\) και \(N\) συμπεριλαμβανομένων. Το ζεύγος αυτό σημαίνει ότι υπάρχει ένας δρόμος που κατευθύνεται από την πόλη \(A\) στην πόλη \(B\). Σε κάθε δρόμο θα είναι \(A \neq B\) αλλά ενδέχεται να υπάρχουν περισσότεροι δρόμοι μεταξύ των ίδιων πόλεων.

Αρχεία Εξόδου (shades.out):

Η έξοδος πρέπει να αποτελείται από μία γραμμή που να περιέχει ακριβώς \(N\) ακέραιους αριθμούς χωρισμένους ανά δύο με ένα κενό διάστημα. Κάθε αριθμός θα αντιστοιχεί σε μία πόλη, κατά σειρά, και θα είναι \(1\) αν αυτή η πόλη είναι τυχερή, διαφορετικά \(0\).

Παράδειγμα Αρχείου Εισόδου - Εξόδου:

shades.in	shades.out
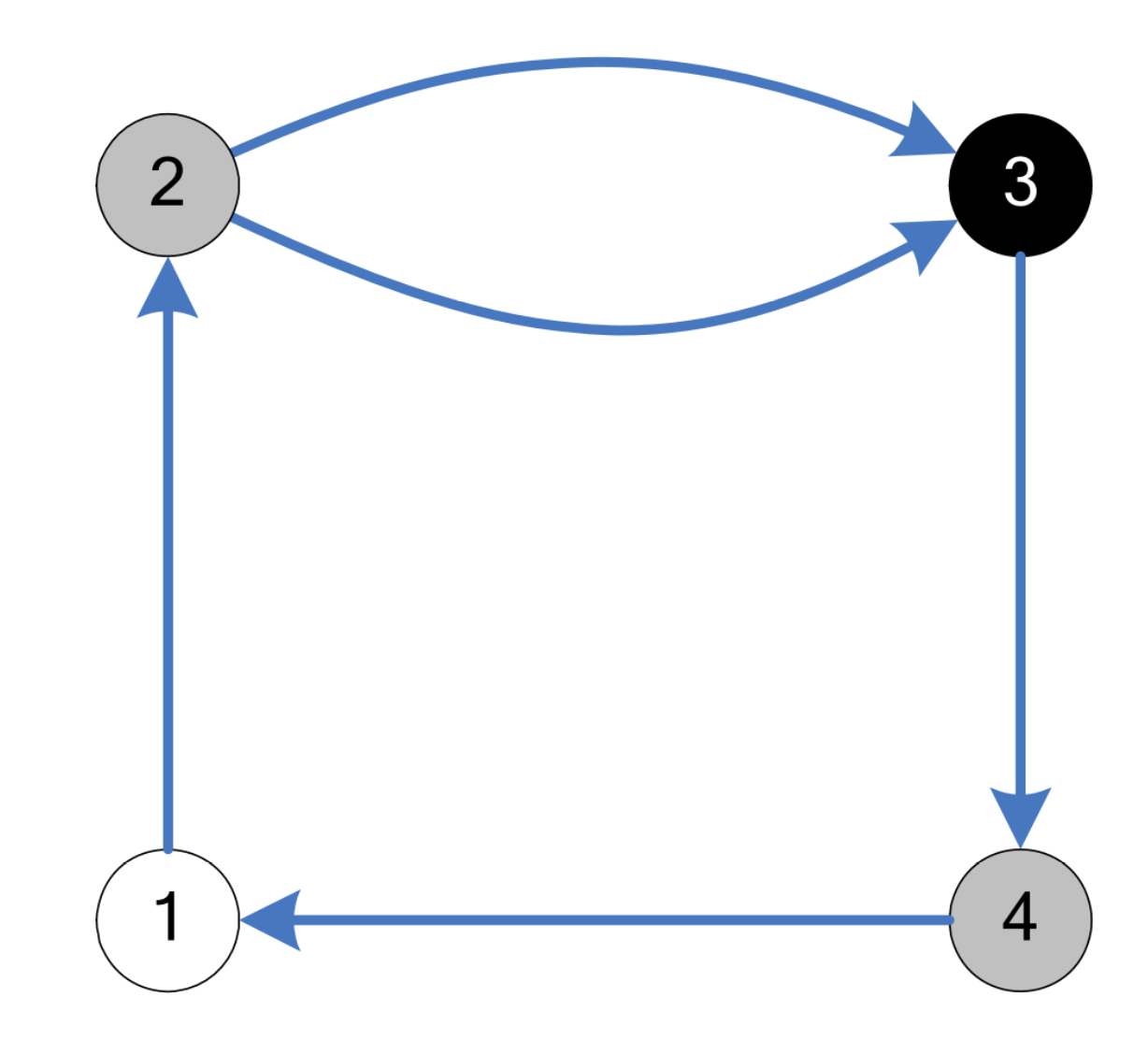
4 5 0 2 1 2 1 2 2 3 3 4 4 1 2 3	1 1 1 0

Εξήγηση παραδείγματος: Στη διαδρομή \(1 \to 2 \to 3\) η αρχική πόλη είναι αγροτική (άσπρη) και η τελική αστική (μαύρη), χωρίς να μεσολαβεί άλλη αστική (μαύρη) πόλη, άρα και οι τρεις αυτές πόλεις είναι τυχερές. Δεν υπάρχει διαδρομή με αυτή την ιδιότητα που να περιέχει την πόλη \(4\), άρα αυτή δεν είναι τυχερή.

Περιορισμοί:

• \(1 \leq N, M \leq 100.000\).
• Όριο χρόνου εκτέλεσης: \(2\) sec.
• Όριο μνήμης: \(128\) MB.