25ος ΠΔΠ Α' Φάση
Αναζητώντας εξωγήινη νοημοσύνη (seti)

Η αναπαράσταση ενός σήματος στο πεδίο των συχνοτήτων αποτελεί το φάσμα του. Εξαιρετικά σημαντική είναι η παρατήρηση ότι τα τεχνητά σήματα (τα σήματα δηλαδή που παράγονται από τεχνητά κατασκευασμένα συστήματα), έχουν μια μοναδική χαρακτηριστική κατανομή φάσματος. Η κατανομή αυτή ονομάζεται και χαρακτηριστική τριπλέτα επειδή συμμετρικά και εκατέρωθεν μιας δεδομένης συχνότητας, (χαρακτηριστική συχνότητα), εμφανίζονται δύο σήματα ίδιας ισχύος, και μάλιστα μικρότερης από το 50% της ισχύος του σήματος που αντιστοιχεί στη χαρακτηριστική συχνότητα.

Το Πανεπιστήμιο του Berkeley (California U.S.A.) έχει αναπτύξει ένα διεθνές πρόγραμμα επεξεργασίας σημάτων από εθελοντές χρήστες του Διαδικτύου, που αποσκοπεί στην αναζήτηση εξωγήινης νοημοσύνης και βασίζεται στην ανάλυση των σημάτων που συλλέγονται από ραδιοτηλεσκόπια (http://setiathome.berkeley.edu/). Το Berkeley συλλέγει τα σήματα από τα ραδιοτηλεσκόπια και, αφού κάνει μια αρχική επεξεργασία, τα διανέμει στους συμμετέχοντες στο πρόγραμμα για να τα επεξεργαστούν. Αυτό που σας ζητείται σε αυτό το πρόβλημα είναι μία πολύ απλοποιημένη εκδοχή της επεξεργασίας που οι συμμετέχοντες καλούνται να κάνουν.

Πρόβλημα

Nα αναπτύξετε ένα πρόγραμμα σε μια από τις γλώσσες του IOI το οποίο θα διαβάζει τις τιμές που αντιστοιχούν σε ένα σήμα και θα αναγνωρίζει τις χαρακτηριστικές συχνότητες.

Mία τριπλέτα σε ένα σήμα είναι μία τριάδα τιμών του σήματος με τις εξής ιδιότητες: (α) οι δύο ακραίες τιμές ισαπέχουν από τη μεσαία τιμή, και (β) οι δύο ακραίες τιμές είναι ίσες μεταξύ τους και μικρότερες του μισού της μεσαίας τιμής. Για παράδειγμα, η τριάδα τιμών που φαίνονται με έντονα γράμματα παρακάτω, είναι τριπλέτα:

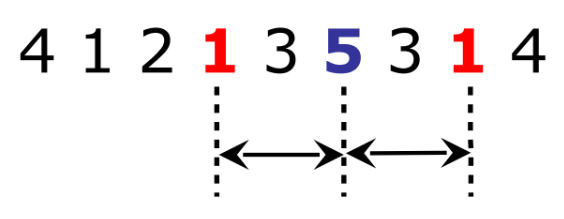
Παράδειγμα

Η μεσαία τιμή μίας τριπλέτας μας δίνει τη χαρακτηριστική συχνότητα, η οποία ισούται με τη θέση της μεσαίας τιμής στο σήμα. Στο παραπάνω παράδειγμα, η χαρακτηριστική συχνότητα είναι \(6\) (γιατί η μεσαία τιμή \(5\), είναι ο έκτος αριθμός που εμφανίζεται στο σήμα).

Αρχεία εισόδου

Τα αρχεία εισόδου με όνομα seti.in είναι αρχεία κειμένου με την εξής δομή: Έχουν ακριβώς δύο γραμμές. Η πρώτη έχει έναν ακέραιο αριθμό \(N\) (\(10 \leq N \leq 10.000\)), που αντιστοιχεί στο πλήθος των τιμών του σήματος που έχουμε καταχωρήσει. Η δεύτερη γραμμή έχει \(N\) ακέραιους αριθμούς χωρισμένους ανά δύο με ένα κενό διάστημα.

Αρχεία εξόδου

Τα αρχεία εξόδου με όνομα seti.out είναι αρχεία κειμένου με την εξής δομή: Η πρώτη γραμμή έχει έναν ακέραιο αριθμό \(K\) (\(0 \leq K \leq N\)). Ο αριθμός αυτός εκφράζει το πλήθος των χαρακτηριστικών συχνοτήτων που εντοπίστηκαν. Ακολουθούν \(K\) γραμμές, κάθε μια από τις οποίες έχει έναν ακέραιο αριθμό \(M\), (\(2 \leq M \leq N-1\)). Ο αριθμός \(M\) εκφράζει μία χαρακτηριστική συχνότητα, δηλαδή τη θέση της μεσαίας τιμής της αντίστοιχης τριπλέτας μέσα στο σήμα (η αρίθμηση αρχίζει από το 1). Οι χαρακτηριστικές συχνότητες πρέπει να δίνονται σε αύξουσα σειρά. Αν σε μία χαρακτηριστική συχνότητα αντιστοιχούν περισσότερες τριπλέτες, η συχνότητα θα πρέπει να εμφανίζεται μόνο μία φορά.

Παράδειγμα αρχείων εισόδου - εξόδου

1^o

seti.in	seti.out
20 1 2 5 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2	1 3

Εξήγηση: υπάρχει μόνο μία τριπλέτα

1 2 5 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

2^o

seti.in	seti.out
25 4 4 5 5 5 6 6 6 6 7 7 7 6 6 6 6 5 5 5 4 4 3 2 1 0	0

Εξήγηση: δεν υπάρχει καμία τριπλέτα

3^o

seti.in	seti.out
12 1 2 2 5 3 2 1 6 1 2 1 4	3 4 5 8

Εξήγηση: υπάρχουν τρεις χαρακτηριστικές συχνότητες

1 2 2 5 3 2 1 6 1 2 1 4 και 1 2 2 5 3 2 1 6 1 2 1 4
1 2 2 5 3 2 1 6 1 2 1 4
1 2 2 5 3 2 1 6 1 2 1 4 και 1 2 2 5 3 2 1 6 1 2 1 4

Όρια