25ος ΠΔΠ Καμπ (κοινά)
Συνάντηση αυτοκινήτων (carmeet)

Έστω ένας κυκλικός δρόμος, πάνω στον οποίο βρίσκονται \(N\) πόλεις, αριθμημένες από \(0\) μέχρι \(N-1\). Ο δρόμος που τις ενώνει είναι μονόδρομος με κατεύθυνση όπως στο παρακάτω σχήμα.

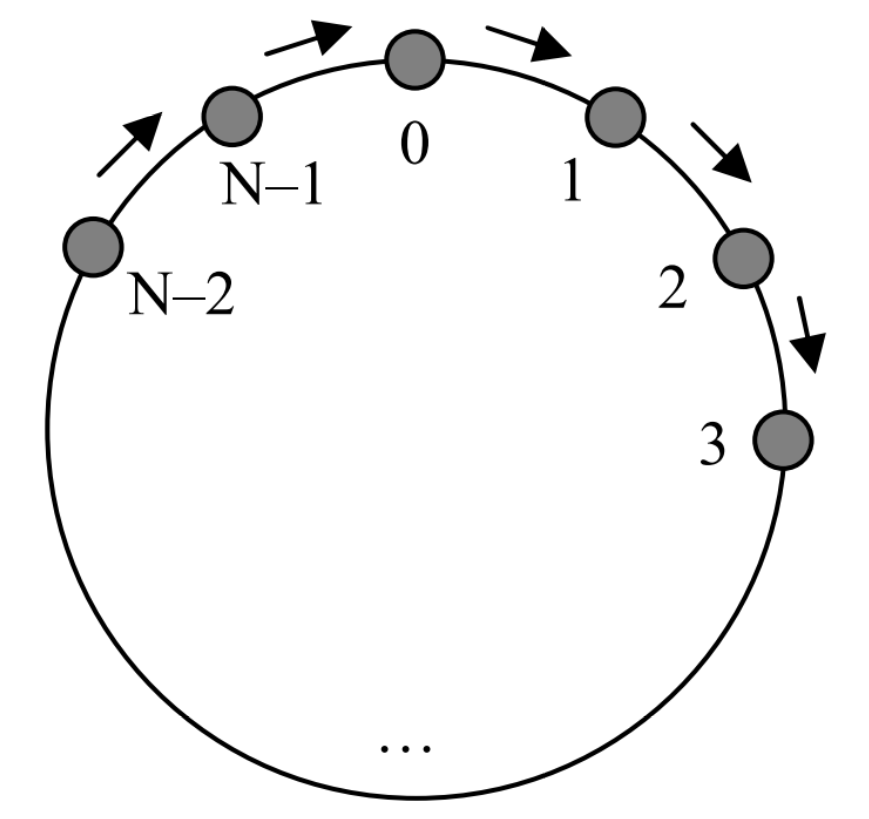
Αναπαράσταση του κυκλικού δρόμου που συνδέει τις N πόλεις

Κατά μήκος του δρόμου, σε κάποιες από τις πόλεις, βρίσκονται συνολικά \(K\) οχήματα. Σε κάθε πόλη μπορούν να βρίσκονται κανένα, ένα ή περισσότερα οχήματα.

Ονομάζουμε κίνηση τη μετακίνηση ενός οχήματος από την πόλη όπου βρίσκεται στην αμέσως επόμενη πάνω στον κύκλο. Μία κίνηση είναι νόμιμη αν στην αμέσως προηγούμενη κίνηση (εφόσον υπάρχει) κινήθηκε διαφορετικό όχημα. Δηλαδή, απαγορεύεται να κινηθεί το ίδιο όχημα δύο διαδοχικές φορές.

Γράψτε ένα πρόγραμμα, το οποίο θα υπολογίζει τον ελάχιστο αριθμό νόμιμων κινήσεων που απαιτούνται ώστε να μετακινηθούν όλα τα οχήματα στην ίδια πόλη. Το πρόγραμμά σας θα πρέπει επίσης να υπολογίζει την πόλη στην οποία θα γίνει η τελική συνάντηση των οχημάτων.

Αρχεία Εισόδου (carmeet.in):

Η είσοδος θα αποτελείται από μόνο δύο γραμμές. Η πρώτη γραμμή περιέχει τους αριθμούς \(N\) (πλήθος πόλεων) και \(K\) (πλήθος οχημάτων), χωρισμένους με ένα κενό διάστημα. Η δεύτερη γραμμή περιέχει \(K\) αριθμούς, που καθορίζουν σε ποιες πόλεις βρίσκονται αρχικά τα \(K\) οχήματα.

Αρχεία Εξόδου (carmeet.out):

Η έξοδος πρέπει να αποτελείται από μία γραμμή που να περιέχει μόνο δύο αριθμούς, χωρισμένους με ένα κενό διάστημα. Ο πρώτος αριθμός θα είναι το πλήθος των ελάχιστων νόμιμων κινήσεων που απαιτούνται για να μετακινηθούν όλα τα οχήματα στην ίδια πόλη. Ο δεύτερος θα είναι ο αριθμός της πόλης στην οποία θα συναντηθούν. Αν είναι δυνατές περισσότερες λύσεις με τον ίδιο ελάχιστο αριθμό κινήσεων, πρέπει να εκτυπώνεται η πόλη συνάντησης με το μικρότερο αριθμό.

Παράδειγμα Αρχείου Εισόδου - Εξόδου:

carmeet.in	carmeet.out
5 4 2 0 2 2	6 3

Εξήγηση παραδείγματος: Τρία από τα τέσσερα οχήματα είναι στην πόλη \(2\) και το τέταρτο είναι στην πόλη \(0\).

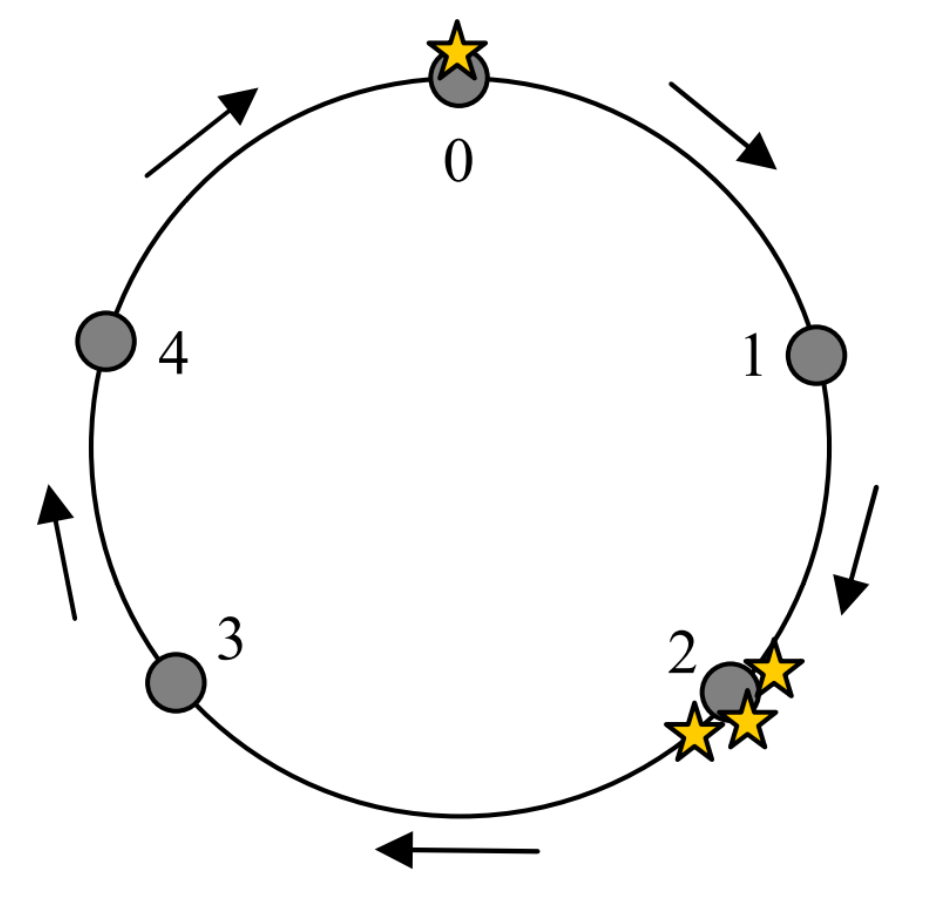
Κυκλική διαδρομή με 5 πόλεις όπου η πόλη 0 έχει 1 όχημα και η πόλη 2 έχει 3.

Τα οχήματα του παραπάνω σχήματος μπορούν να συναντηθούν μετά από \(6\) νόμιμες κινήσεις στην πόλη \(3\). (Μία ακολουθία κινήσεων που οδηγεί σε αυτή τη λύση είναι να κινούνται εναλλάξ το όχημα που ξεκίνησε από την πόλη \(0\) και ένα όχημα από την πόλη \(2\).)

Περιορισμοί:

\(1 \leq N \leq 10.000\).
\(1 \leq K \leq 10.000\).
Όριο χρόνου εκτέλεσης: \(2\) sec.
Όριο μνήμης: \(64\) MB.

Subtasks