26ος ΠΔΠ Γ' Φάση
Μετατροπή αριθμού (numbase)

Ένα από τα πρώτα μαθήματα των σπουδαστών της Πληροφορικής είναι η αναπαράσταση των φυσικών αριθμών στο δυαδικό σύστημα αρίθμησης (βάση το \(2\)). Το σύστημα αυτό χρησιμοποιεί μόνο δύο ψηφία, το \(0\) και το \(1\).

Στην καθημερινότητα χρησιμοποιούμε για λόγους ευκολίας το δεκαδικό σύστημα (βάση το \(10\)) που χρησιμοποιεί δέκα ψηφία, από \(0\) έως και \(9\). Γενικά θα μπορούσαμε να χρησιμοποιήσουμε οποιοδήποτε σύστημα αρίθμησης. Για παράδειγμα οι πληροφορικοί χρησιμοποιούν συχνά τα συστήματα με βάση το \(8\) ή το \(16\). Στο σύστημα αρίθμησης με βάση \(K\) χρησιμοποιούνται \(K\) ψηφία με αξία από \(0\) έως και \(K−1\).

Έστω ότι δίνεται ένας φυσικός αριθμός \(M\), γραμμένος στο δεκαδικό σύστημα. Για τη μετατροπή του στην αντίστοιχη γραφή στο σύστημα με βάση το \(K\), διαιρούμε διαδοχικά τον \(M\) με το \(K\) μέχρι να φτάσουμε σε πηλίκο που είναι μικρότερο από το \(K\). Η αναπαράσταση του \(M\) στο σύστημα με βάση το \(K\) σχηματίζεται από το τελικό πηλίκο (σαν πρώτο ψηφίο) και ακολουθείται από τα υπόλοιπα των διαιρέσεων που προηγήθηκαν. Για παράδειγμα για \(M=122\) και \(K=8\):

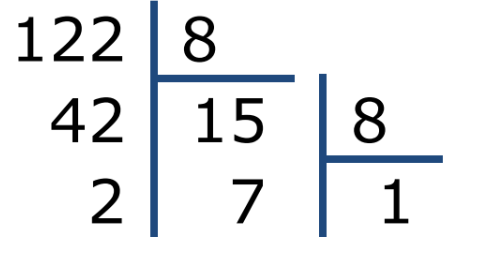
Δηλαδή \(122_{10}=172_8\) (ο αριθμός \(122\) στο δεκαδικό σύστημα είναι ίσος με \(172\) στο οκταδικό σύστημα: \(172_8=1\times 8^2+7\times 8+2=122\)). Ένας σπουδαστής έκανε την εξής παρατήρηση: εφαρμόζοντας τον παραπάνω κανόνα μετατροπής φυσικών αριθμών σε άλλο σύστημα αρίθμησης, σε κάποιες περιπτώσεις στη νέα αναπαράσταση όλα τα ψηφία του αριθμού είναι ίδια. Για παράδειγμα \(63_{10} = 333_4\).

Πρόβλημα

Nα γραφεί ένα πρόγραμμα σε μια από τις γλώσσες του ΙΟΙ το οποίο, όταν δίδεται ένας αριθμός \(M\) στη δεκαδική του αναπαράσταση, να βρίσκει την ελάχιστη βάση \(B\) έτσι ώστε στην αναπαράσταση του \(M\) στη βάση \(B\) όλα τα ψηφία να είναι ίδια.

Aρχεία εισόδου

Τα αρχεία εισόδου με όνομα numbase.in είναι αρχεία κειμένου με την εξής δομή: Στην πρώτη γραμμή έχουν ένα φυσικό αριθμό \(N\) (\(1 \leq N \leq 10\)), το πλήθος των αριθμών που θα ακολουθήσουν. Ακολουθούν \(N\) γραμμές, κάθε μία από τις οποίες περιέχει ένα φυσικό αριθμό \(M_k\) (\(1 \leq M_k \leq 10^{12}\) όπου \(1 \leq k \leq N\)).

Aρχεία εξόδου

Τα αρχεία εξόδου με όνομα numbase.out είναι αρχεία κειμένου με την εξής δομή: Έχουν \(N\) γραμμές που κάθε μία περιέχει μόνο έναν ακέραιο αριθμό \(B_k\) (\(2 \leq B_k\) όπου \(1 \leq k \leq N\)). Το \(B_k\) πρέπει να είναι η ελάχιστη βάση ώστε η αναπαράσταση του αριθμού \(M_k\) να έχει όλα του τα ψηφία ίδια.

Παράδειγμα αρχείων εισόδου - εξόδου

numbase.in	numbase.out
5 7 42 63 2 630	2 4 2 3 29

Βαθμολογία:

• Στο 30% των περιπτώσεων ελέγχου θα είναι \(M_k \leq 10^3\)
• Στο 50% των περιπτώσεων ελέγχου θα είναι \(M_k \leq 10^6\)
• Στο 75% των περιπτώσεων ελέγχου θα είναι \(M_k \leq 10^9\)

Προσοχή: για το 25% των περιπτώσεων ελέγχου θα χρειαστείτε αριθμούς των 64 bit (long long ή int64_t στη GNU C/C++, Int64 στη Free Pascal).

Mορφοποίηση: Στην έξοδο, όλες οι γραμμές τερματίζουν με ένα χαρακτήρα newline.
Mέγιστος χρόνος εκτέλεσης: \(1\) sec.
Mέγιστη διαθέσιμη μνήμη: \(64\) MB.