27ος ΠΔΠ Γ' Φάση
Εφημερίδες (efimerides)

[30 Μονάδες]

Ο Πέτρος μοιράζει τον ημερήσιο τύπο. Πρέπει να επισκεφθεί \(N\) σημεία πώλησης, τοποθετημένα σε μία κυκλική διαδρομή. Γνωρίζει ότι το \(i\)-οστό σημείο πώλησης του αφήνει κέρδος \(A_i\). Αν όμως αρχίσει να επισκέπτεται τα \(N\) σημεία με τη σειρά, τότε σε κάποιες περιοχές ο τύπος θα φτάσει έγκαιρα σε όλα τα σημεία πώλησης, ενώ σε κάποιες άλλες περιοχές ο τύπος θα αργήσει να φτάσει.

Ο Πέτρος αποφασίζει λοιπόν να ξεκινάει από κάποιο σημείο πώλησης \(i\), να αφήνει εκεί τις εφημερίδες και στη συνέχεια, κινούμενος κυκλικά, να προσπερνάει \(K−1\) σημεία και να πηγαίνει στο επόμενο σημείο για να αφήσει την εκεί ζήτηση. Αφήνει δηλαδή εφημερίδες κάθε \(K\) σημεία, αρχίζοντας από το \(i\). Το μόνο πρόβλημα είναι ότι έτσι του είναι δύσκολο να θυμάται πού έχει πάει και πού όχι. Αποφασίζει λοιπόν να σταματάει όταν φθάσει σε ένα σημείο όπου έχει ήδη αφήσει εφημερίδες. Έτσι, είναι πιθανό όταν σταματήσει να μην έχει επισκεφθεί όλα τα σημεία πώλησης.

Πρόβλημα

Nα γραφεί ένα πρόγραμμα σε μια από τις γλώσσες του ΙΟΙ το οποίο να διαβάζει τις τιμές του \(N\) και του \(K\) και τα κέρδη \(A_i\) και να βρίσκει το μεγαλύτερο συνολικό κέρδος που μπορεί να έχει ο Πέτρος, ακολουθώντας αυτή τη διαδικασία.

Aρχεία εισόδου

Τα αρχεία εισόδου με όνομα efimerides.in είναι αρχεία κειμένου αποτελούμενα από δύο γραμμές: Στην πρώτη γραμμή δίνονται δύο ακέραιοι χωρισμένοι μεταξύ τους με ένα κενό διάστημα: οι τιμές των \(N\) και \(K\) (\(2 \leq K \leq N \leq 1.000.000\)). Στη δεύτερη γραμμή δίνονται \(N\) ακέραιοι αριθμοί \(A_i\) (\(1 \leq A_i \leq 1.000.000\)), χωρισμένοι ανά δύο με ένα κενό διάστημα: οι όροι της ακολουθίας. Το άθροισμα όλων των \(A_i\) δε θα υπερβαίνει το \(1.000.000.000\).

Aρχεία εξόδου

Τα αρχεία εξόδου με όνομα efimerides.out είναι αρχεία κειμένου αποτελούμενα από ακριβώς μία γραμμή που περιέχει ακριβώς έναν ακέραιο αριθμό: το μέγιστο δυνατό κέρδος του Πέτρου.

Παραδείγματα αρχείων εισόδου - εξόδου

1^ο:

efimerides.in	efimerides.out
5 2 1 2 3 4 5	15

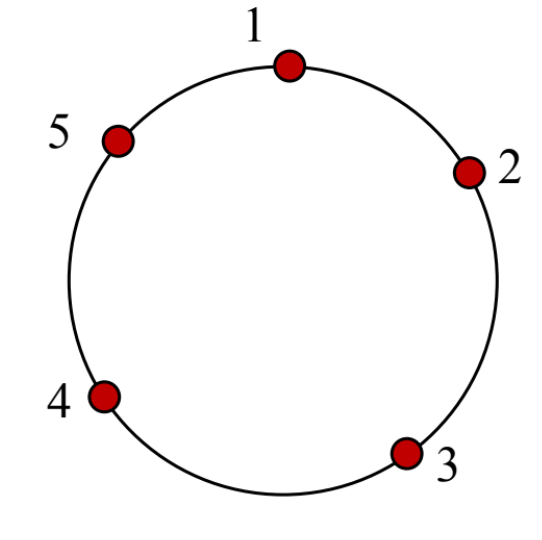
Εξήγηση: Στο πρώτο παράδειγμα, απ’ όπου κι αν ξεκινήσει ο Πέτρος θα επισκεφθεί όλα τα σημεία πώλησης. Επομένως το συνολικό του κέρδος θα είναι ίσο με το συνολικό άθροισμα. Μια δυνατή διαδρομή με αυτό το συνολικό κέρδος είναι: \(1 + 3 + 5 + 2 + 4 = 15\).

Παράδειγμα 1

2^ο:

efimerides.in	efimerides.out
6 3 4 1 3 6 2 7	10

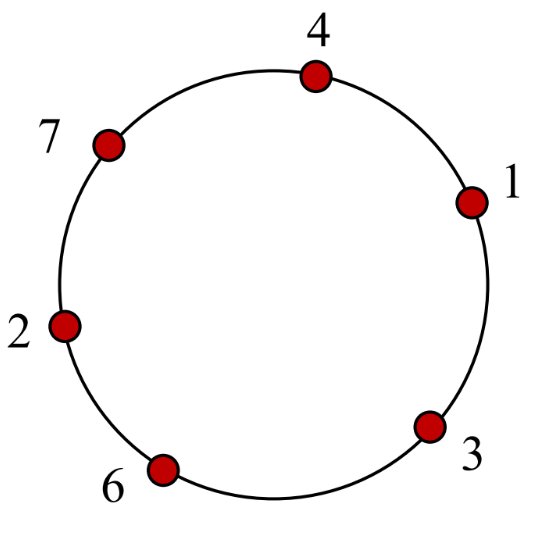
Εξήγηση: Στο δεύτερο παράδειγμα το σημείο από το οποίο ξεκινάει έχει σημασία. Αν π.χ. ξεκινήσει από το \(2\), θα έχει κέρδος \(2 + 1 = 3\), ενώ αν ξεκινήσει από το \(4\), θα έχει κέρδος \(4 + 6 = 10\). Το μέγιστο δυνατό κέρδος είναι \(10\) και μπορεί να το πάρει με άλλους, διαφορετικούς τρόπους, π.χ. \(7 + 3 = 10\).

Παράδειγμα 2