28ος ΠΔΠ Καμπ (seniors)
Σημαντικοί Δρόμοι (critical)

Μια ομάδα μηχανικών εργάζεται για τη βελτίωση του οδικού δικτύου μιας χώρας. Ενδιαφέρονται συγκεκριμένα για τους δρόμους μέσω των οποίων φτάνουμε από την πρωτεύουσα προς τις υπόλοιπες πόλεις της χώρας. Στην χώρα υπάρχουν \(N\) πόλεις και \(M\) δρόμοι (μονής κατεύθυνσης) μέσω των οποίων μπορεί κανείς να φθάσει από την πρωτεύουσα προς όλες τις υπόλοιπες πόλεις (είτε απευθείας είτε μέσω ενδιάμεσων πόλεων). Κάθε δρόμος \((x, y)\) που ενώνει μια πόλη \(x\) με μια πόλη \(y\) έχει ένα θετικό ακέραιο μήκος \(w(x, y)\).

Οι μηχανικοί θεωρούν ότι ένας δρόμος είναι σημαντικός όταν η μείωση του μήκους του κατά μία μονάδα επιφέρει αντίστοιχη μείωση στην απόσταση της πρωτεύουσας προς κάποια άλλη πόλη, και πολύ σημαντικός όταν η αύξηση του μήκους του κατά μία μονάδα επιφέρει αντίστοιχη αύξηση στην απόσταση της πρωτεύουσας προς κάποια άλλη πόλη. Θέλουν λοιπόν να υπολογίσουν πόσοι δρόμοι είναι σημαντικοί και πόσοι δρόμοι είναι πολύ σημαντικοί στο οδικό δίκτυο της χώρας.

Γράψτε ένα πρόγραμμα που να υπολογίζει το πλήθος των σημαντικών και των πολύ σημαντικών δρόμων.

Αρχεία Εισόδου (critical.in):

Η πρώτη γραμμή της εισόδου θα περιέχει δύο φυσικούς αριθμούς \(N\) και \(M\): το πλήθος των πόλεων και το πλήθος των δρόμων. Κάθε μία από τις επόμενες \(M\) γραμμές της εισόδου θα περιέχει τρεις φυσικούς αριθμούς \(x\), \(y\) και \(w(x, y)\), χωρισμένους μεταξύ τους με ένα κενό διάστημα, που δηλώνουν ότι υπάρχει δρόμος μήκους \(w(x, y)\) που συνδέει την πόλη \(x\) με την πόλη \(y\).

Θεωρήστε ότι οι πόλεις είναι αριθμημένες από \(1\) μέχρι και \(N\), ότι η πρωτεύουσα είναι η πόλη με αριθμό \(1\), ότι όλοι οι δρόμοι είναι μονής κατεύθυνσης και ότι κάθε δρόμος θα εμφανίζεται μία μόνο φορά. Θεωρήστε ακόμη ότι από την πρωτεύουσα θα μπορούμε πάντα να φθάσουμε σε όλες τις υπόλοιπες πόλεις.

Αρχεία Εξόδου (critical.out):

Η έξοδος πρέπει να αποτελείται από μία γραμμή που θα περιέχει δύο φυσικούς αριθμούς χωρισμένους με ένα κενό μεταξύ τους: το πλήθος των σημαντικών δρόμων και το πλήθος των πολύ σημαντικών δρόμων.

Παράδειγμα Αρχείου Εισόδου - Εξόδου:

critical.in	critical.out
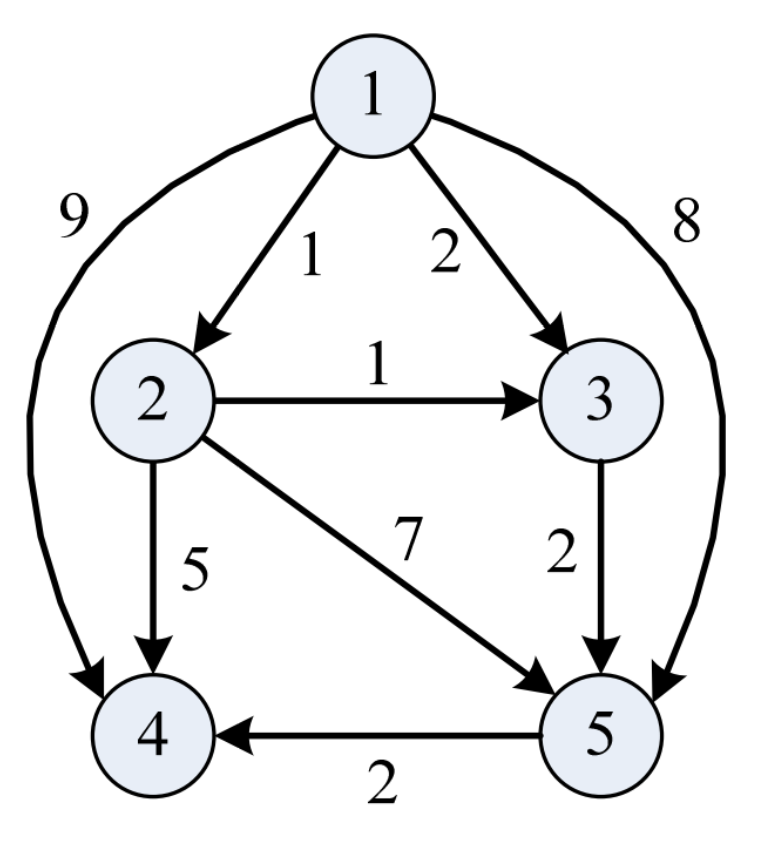
5 9 1 2 1 1 3 2 1 4 9 1 5 8 2 3 1 2 4 5 2 5 7 3 5 2 5 4 2	6 2

Εξήγηση παραδείγματος: Οι δρόμοι \((1, 2)\), \((1, 3)\), \((2, 3)\), \((2, 4)\), \((3, 5)\) και \((5, 4)\) είναι σημαντικοί (\(6\) δρόμοι συνολικά). Π.χ., η μείωση του μήκους του δρόμου \((1, 2)\) από \(1\) σε \(0\) μειώνει την απόσταση της πρωτεύουσας προς την πόλη \(2\) από \(1\) σε \(0\). Ομοίως, η μείωση του μήκους του δρόμου \((2, 3)\) από \(1\) σε \(0\) μειώνει την απόσταση της πρωτεύουσας προς την πόλη \(3\) από \(2\) σε \(1\). Κάτι αντίστοιχο ισχύει και για τους δρόμους \((2, 3)\), \((2, 4)\), \((3, 5)\) και \((5, 4)\).

Οι δρόμοι \((1, 2)\) και \((3, 5)\) είναι πολύ σημαντικοί (\(2\) δρόμοι συνολικά). Π.χ., η αύξηση του μήκους του δρόμου \((1, 2)\) από \(1\) σε \(2\) αυξάνει την απόσταση της πρωτεύουσας προς την πόλη \(2\) από \(1\) σε \(2\). Ομοίως, η αύξηση του μήκους του δρόμου \((3, 5)\) από \(2\) σε \(3\) αυξάνει την απόσταση της πρωτεύουσας προς την πόλη \(5\) από \(4\) σε \(5\).

Περιορισμοί

• \(2 \leq N \leq 40.000\).
• \(N - 1 \leq M \leq 400.000\).
• \(1 \leq w(x, y) \leq 1.000\).
• Όριο χρόνου εκτέλεσης: \(1\) sec.
• Όριο μνήμης: \(64\) MB.