30ος ΠΔΠ Γ' Φάση
Ο Χρήστος και τα τούβλα (brickbreaker)

Ο Χρήστος είναι Πολιτικός Mηχανικός. Η πτυχιακή του εργασία αφορά την αστοχία των υλικών στα κτίρια. Συγκεκριμένα, ο Χρήστος προσομοιώνει την κατασκευή ενός τοίχου σαν ένα πλέγμα διαστάσεων \(N \times M\), του οποίου κάθε τετραγωνάκι μπορεί να περιέχει ένα τούβλο (που συμβολίζεται με “#”) ή να είναι κενό (που συμβολίζεται με “.”). Στην κορυφή του πλέγματος, την οποία μπορείτε να φαντάζεστε σαν το ταβάνι, υπάρχει μια στρώση μπετόν και επομένως όσα τούβλα βρίσκονται στην πιο πάνω γραμμή του πλέγματος είναι κολλημένα στο ταβάνι και δεν πέφτουν. Όλα τα τούβλα έχουν μπετόν σε κάθε πλευρά τους και άρα όσα ακουμπάνε σε τούβλα της πιο πάνω γραμμής επίσης δεν πέφτουν, όσα ακουμπάνε σε αυτά επίσης δεν πέφτουν, κ.ο.κ. Θεωρούμε πως ένα τούβλο μπορεί να ακουμπάει σε άλλα τούβλα που βρίσκονται στα τέσσερα γειτονικά τετράγωνα του πλέγματος: αριστερά, δεξιά, πάνω και κάτω.

Ο Χρήστος θέλει να μελετήσει τη συμπεριφορά του τοίχου αν κάποια τούβλα “αστοχήσουν”. Συγκεκριμένα, θέλει να κάνει το εξής πείραμα: Επιλέγει ένα σύνολο από τούβλα-στόχους και πηγαίνει και τα σπάει, ένα-ένα. Κάθε φορά που σπάει ένα τούβλο-στόχος, είναι πιθανό ένα κομμάτι της κατασκευής να καταρρεύσει, αφού πλέον δεν θα συνδέεται με το υπόλοιπο στέρεο κομμάτι. Ο Χρήστος θέλει να ξέρει κάθε φορά που σπάει ένα τούβλο-στόχο πόσο μεγάλο θα είναι το κομμάτι που καταρρέει, δηλαδή πόσα τούβλα περιέχει.

Πρόβλημα

Nα αναπτύξετε ένα πρόγραμμα σε μια από τις γλώσσες της IOI (Pascal, C, C++, Java) το οποίο θα διαβάζει την αρχική κατάσταση του πλέγματος και το σύνολο των τούβλων-στόχων και θα βρίσκει το πλήθος των τούβλων που καταρρέουν μετά από κάθε σπάσιμο.

Αρχεία εισόδου

Το αρχείο εισόδου με όνομα brickbreaker.in είναι αρχείο κειμένου. Η πρώτη γραμμή περιέχει δύο ακεραίους \(N\) και \(M\) χωρισμένους μεταξύ τους με ένα κενό διάστημα: τον αριθμό των γραμμών και των στηλών του πλέγματος αντίστοιχα. Οι επόμενες \(N\) γραμμές περιέχουν την περιγραφή του πλέγματος: κάθε μία από αυτές θα περιέχει ακριβώς \(M\) χαρακτήρες, ο καθένας εκ των οποίων θα είναι “#” ή “.” (τελεία) ανάλογα αν το αντίστοιχο τετράγωνο περιέχει τούβλο ή είναι κενό. Η επόμενη γραμμή θα περιέχει έναν ακέραιο αριθμό \(Q\): το πλήθος των τούβλων-στόχων που θα σπάσει ο Χρήστος. Κάθε μία από τις επόμενες \(Q\) γραμμές περιέχει δύο ακέραιους αριθμούς \(R_i\) και \(C_i\): τις συντεταγμένες στο πλέγμα (γραμμή και στήλη) του αντίστοιχου τούβλου-στόχου. Η αρίθμηση των γραμμών και των στηλών ξεκινά από το \(1\) (η 1^η γραμμή είναι αυτή που ακουμπά στο ταβάνι και η 1^η στήλη είναι η αριστερότερη). Θεωρήστε ότι η αρχική κατασκευή των τούβλων ευσταθεί (δεν πέφτουν τούβλα πριν το πρώτο σπάσιμο!).

Αρχεία εξόδου

Το αρχείο εξόδου με όνομα brickbreaker.out είναι αρχείο κειμένου αποτελούμενο από \(Q\) γραμμές, κάθε μία από τις οποίες θα περιέχει έναν μόνο ακέραιο αριθμό: το πλήθος των τούβλων που θα καταρρεύσουν όταν ο Χρήστος σπάσει το αντίστοιχο τούβλο-στόχο.

Προσοχή: στο μέγεθος του τμήματος της κατασκευής που καταρρέει δεν θα πρέπει να προσμετρήσετε το τούβλο-στόχο, το οποίο σπάει!

Παράδειγμα αρχείων εισόδου - εξόδου

brickbreaker.in	brickbreaker.out
5 5 ##.## ##### ..#.. .###. .#.#. 4 4 2 4 3 2 3 2 5	1 2 1 0

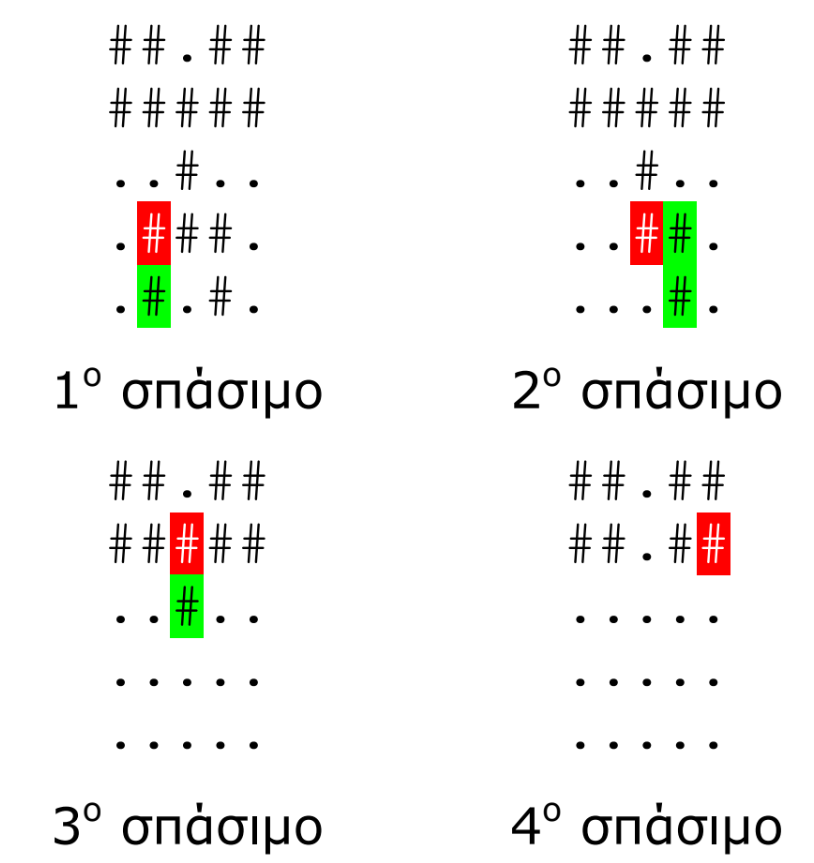
Εξήγηση: Το πρώτο τούβλο-στόχος βρίσκεται στην θέση \((4,2)\). Όταν σπάσει, το μόνο τούβλο που πέφτει είναι το \((5,2)\), συνεπώς η απάντηση είναι \(1\). Στο δεύτερο σπάσιμο πέφτουν τα τούβλα \((4,4)\) και \((5,4)\), στο τρίτο πέφτει το τούβλο \((3,3)\), ενώ στο τέταρτο δεν πρόκειται να πέσει κανένα τούβλο.

Περιορισμοί:

• Το άθροισμα όλων των αριθμών της λίστας δε θα ξεπερνά το \(10^9\).
• Για περιπτώσεις ελέγχου συνολικής αξίας 25%, θα είναι: \(1 \leq N \leq 20\)

• Για περιπτώσεις ελέγχου συνολικής αξίας 100%, θα είναι: \(1 \leq N \leq 10.000\)

• Mορφοποίηση: Στην είσοδο αλλά και στην έξοδο, κάθε γραμμή τερματίζει με έναν χαρακτήρα newline.
• Mέγιστος χρόνος εκτέλεσης: \(1\) sec.
• Mέγιστη διαθέσιμη μνήμη: \(64\) MB.