31ος ΠΔΠ Καμπ (κοινά)
Συνάντηση στην δενδρούπολη (treecity)
Είναι η εποχή του χρόνου που γίνεται το Camp του Πανελλήνιου Διαγωνισμού Πληροφορικής. Για πρώτη φορά φέτος το Camp οργανώνεται στην δενδρούπολη. Η δενδρούπολη είναι μια πραγματική πόλη στην χώρα των αλγορίθμων, η οποία ωστόσο έχει μια ιδιομορφία: μοιάζει με δένδρο (ακυκλικό συνεκτικό γράφημα). Συγκεκριμένα, η δενδρούπολη έχει \(N\) κορυφές, οι οποίες αριθμούνται από το \(1\) μέχρι το \(N\) και κάποιες από αυτές συνδέονται μεταξύ τους με δρόμους διαφόρων αποστάσεων. Είναι σίγουρο πως υπάρχει μοναδικό μονοπάτι μεταξύ οποιουδήποτε ζεύγους κορυφών. Παρατηρείστε πως για να ισχύουν τα παραπάνω, το συνολικό πλήθος των δρόμων πρέπει να είναι \(N−1\).
Φέτος στο Camp έχουμε πολύ κόσμο ο οποίος έχει εγκατασταθεί σε κάποιες κορυφές της δενδρούπολης. Δυστυχώς δεν έχουμε βρει ακόμα πού θα γίνονται τα μαθήματα και γι’ αυτό χρειαζόμαστε την βοήθεια σας. Γνωρίζουμε ακριβώς σε ποιές κορυφές βρίσκονται οι διαγωνιζόμενοι και θέλουμε, προκειμένου να τους βολέψουμε όλους, να βρούμε την κορυφή που ελαχιστοποιεί το άθροισμα αποστάσεων απ’ όλες τις κορυφές στις οποίες βρίσκονται οι διαγωνιζόμενοι.
Αρχεία Εισόδου (treecity.in):
Στην πρώτη γραμμή της εισόδου δίνεται ένας θετικός ακέραιος αριθμός \(N\), το πλήθος των κορυφών της δενδρούπολης. Στην επόμενη γραμμή βρίσκονται \(N\) θετικοί ακέραιοι, ο \(i\)-οστός απ’ τους οποίους είναι \(1\) αν στην \(i\)-οστή κορυφή βρίσκεται κάποιος διαγωνιζόμενος, αλλιώς είναι \(0\). Ακολουθούν \(N−1\) γραμμές, η καθεμία εκ των οποίων περιέχει \(3\) αριθμούς \(u\), \(v\), \(w\). Κάθε τέτοια γραμμή παριστάνει ένα δρόμο ανάμεσα στις κορυφές \(u\) και \(v\), με απόσταση \(w\). Θεωρήσετε δεδομένο πως η τοπολογία που περιγράφεται είναι πράγματι αυτή ενός δένδρου.
Αρχεία Εξόδου (treecity.out):
Να εκτυπώσετε μία γραμμή που να περιέχει έναν θετικό ακέραιο αριθμό: το ελάχιστο άθροισμα των αποστάσεων από κάποια κορυφή της δενδρούπολης προς όλους τους κόμβους όπου βρίσκονται οι διαγωνιζόμενοι.
Παράδειγμα Αρχείου Εισόδου - Εξόδου:
| treecity.in | treecity.out |
|---|---|
| 7 0 0 1 1 1 0 1 1 2 1 1 3 3 1 4 2 2 7 4 3 5 1 3 6 7 |
14 |
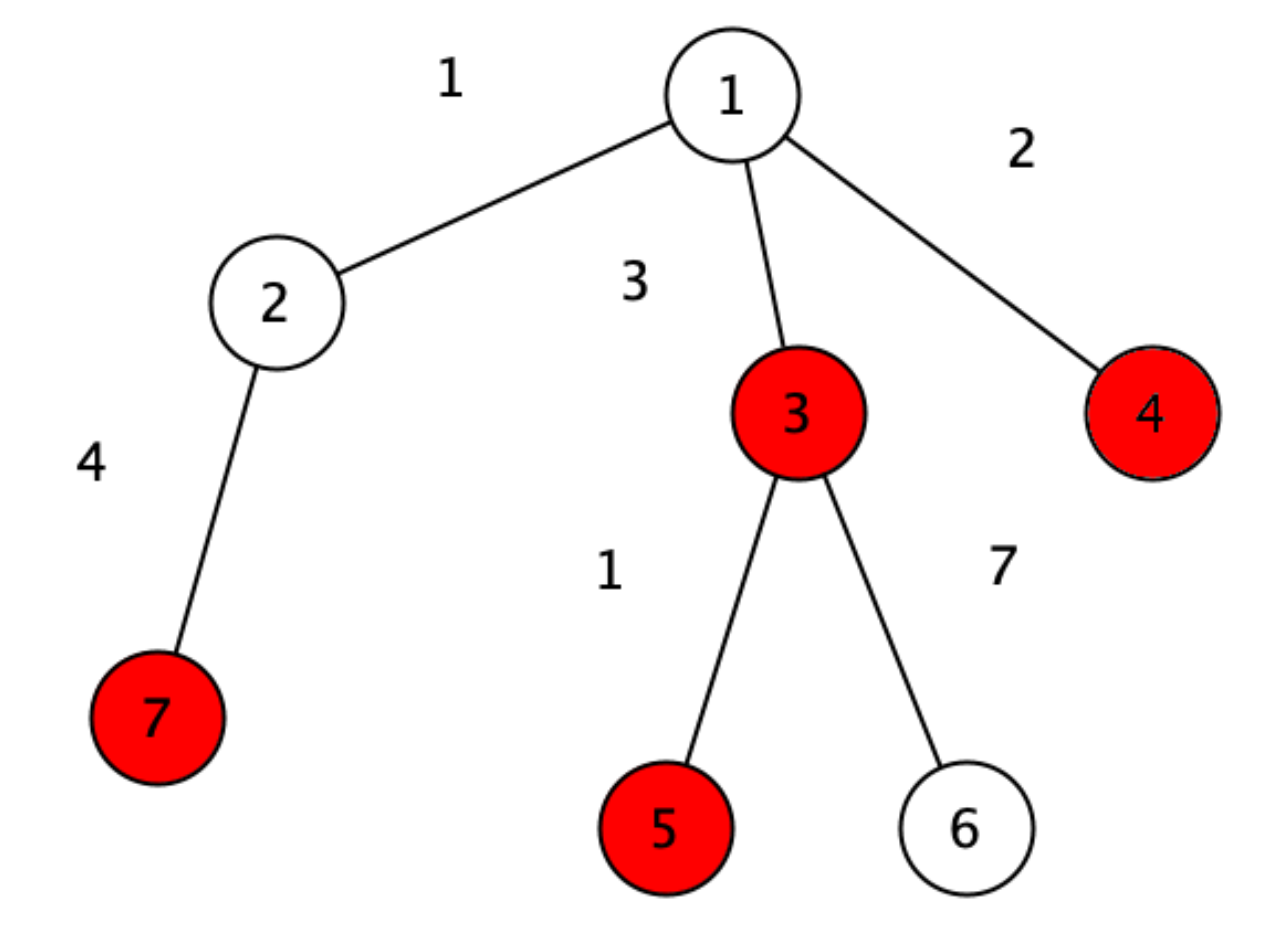
Εξήγηση παραδείγματος: Η μορφή της δενδρούπολης φαίνεται παρακάτω. Υπάρχουν τέσσερις κόκκινες κορυφές, οι \(3\), \(4\), \(5\) και \(7\), στις οποίες βρίσκονται οι διαγωνιζόμενοι. Η βέλτιστη επιλογή που μπορούμε να κάνουμε είναι να βάλουμε τα μαθήματα στην κορυφή \(1\), για την οποία έχουμε απόσταση \(5\) απ’ την κόρυφη \(7\), απόσταση \(3\) από την κορυφή \(3\), απόσταση \(4\) απ’ την κορυφή \(5\) και απόσταση \(2\) απ’την κορυφή \(4\). Συνολικά δηλαδή, το άθροισμα των αποστάσεων των διαγωνιζομένων από αυτή την κορυφή είναι \(5 + 3 + 4 + 2 = 14\). Είναι εύκολο να δούμε πως αυτή ειναι και η βέλτιστη απάντηση.
Subtasks
- Στο 30%, \(1 \leq N \leq 5.000\) (Κανένας επιπλέον περιορισμός).
- Στο 30%, \(1 \leq N \leq 500.000\) (Το πλήθος των κορυφών που μένει κάποιος διαγωνιζόμενος είναι το πολύ \(15\)).
- Στο 40%, \(1 \leq N \leq 500.000\) (Κανένας επιπλέον περιορισμός).