31ος ΠΔΠ Καμπ (juniors)
Παραλληλόγραμμα (parallel)
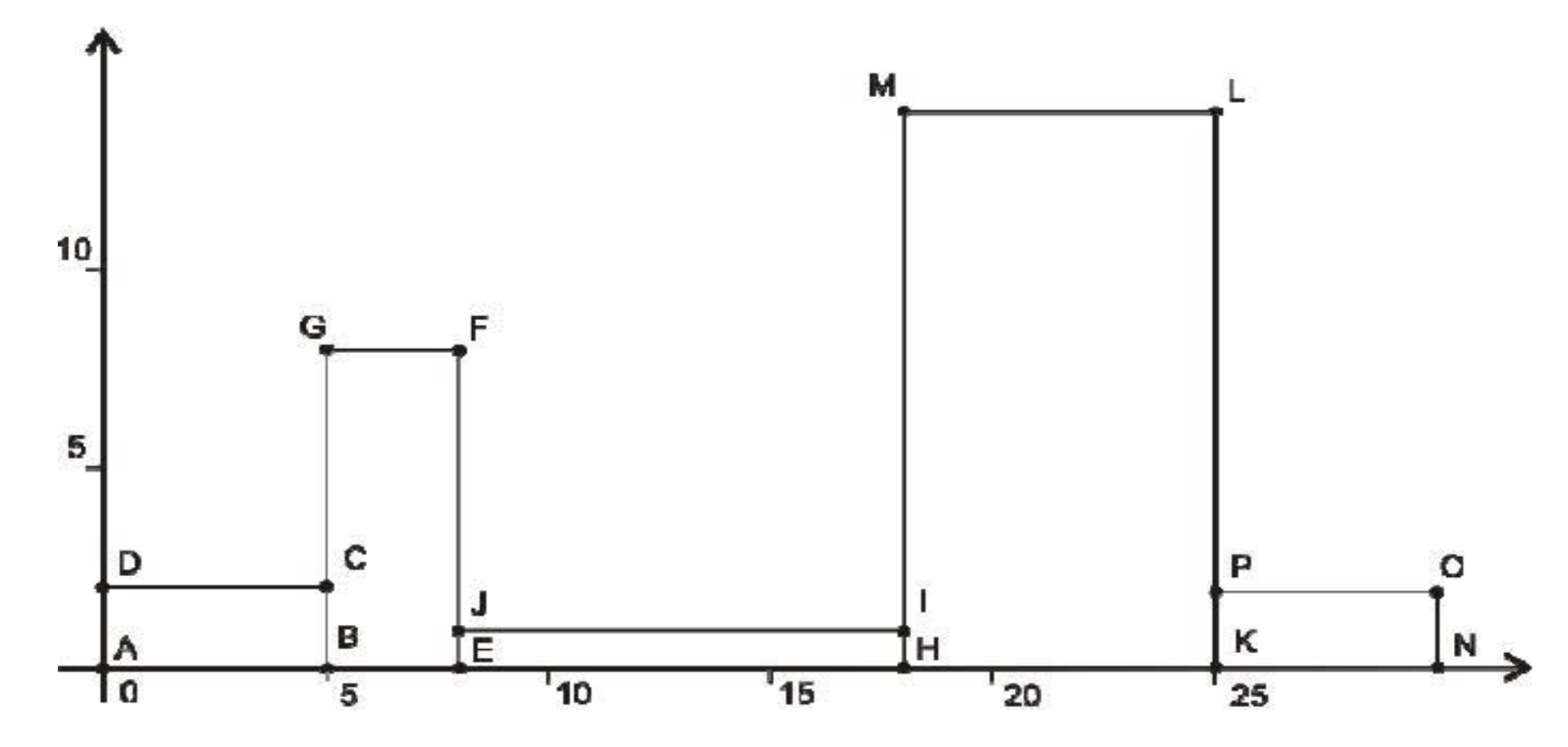
Δίνονται \(N\) παραλληλόγραμμα, αριθμημένα από το \(1\) εώς το \(N\). Κάθε παραλληλόγραμμο \(i\) έχει διαστάσεις \(X_i\) και \(Y_i\) αντίστοιχα. Θέλουμε να διατάξουμε τα παραλληλόγραμμα κατά μήκος του άξονα X το ένα κολλητά δίπλα στο άλλο, χωρίς να αλλάξουμε την σειρά με την οποία δίνονται. Μπορούμε ωστόσο να διαλέξουμε ποια πλευρά του κάθε παραλληλογράμμου θα βάλουμε κατά μήκος του άξονα Χ, προκειμένου να μεγιστοποιήσουμε το μήκος της άνω πολυγωνικής γραμμής του σχήματος. Η άνω πολυγωνική γραμμή του σχήματος που προκύπτει ορίζεται ως η περίμετρος του σχήματος, αν απ’ αυτήν αφαιρέσουμε την αριστερή, την δεξιά και την κάτω πλευρά. Για παράδειγμα στο παρακάτω σχήμα η άνω πολυγωνική γραμμή ορίζεται απ’ τα ευθύγραμμα τμήματα DC, CG, GF, FJ, JI, IM, ML, LP, PO.
Αρχεία Εισόδου (parallel.in):
Στην πρώτη γραμμή της εισόδου δίνεται ένας θετικός ακέραιος αριθμός \(N\), το πλήθος των παραλληλογράμμων που θα μας δοθούν. Ακολουθούν \(N\) γραμμές, η \(i\)-οστή εκοστή εκ των οποίων αποτελείται από δύο θετικούς ακεραίους \(X_i\) και \(Y_i\), τις διαστάσεις του \(i\)-οστή εκοστού παραλληλογράμμου. Θεωρήστε ότι \(1 \leq X_i \leq 1.000\) και \(1 \leq Y_i \leq 1.000\).
Αρχεία Εξόδου (parallel.out):
Να εκτυπώσετε έναν θετικό ακέραιο: Το μέγιστο μήκος της άνω πολυγωνικής γραμμής που μπορεί να προκύψει από κάθε πιθανή διάταξη των παραλληλογράμμων στον άξονα Χ.
Παράδειγμα Αρχείου Εισόδου - Εξόδου:
| parallel.in | parallel.out |
|---|---|
| 5 2 5 3 8 1 10 7 14 2 5 |
68 |
Εξήγηση παραδείγματος: Το παράδειγμα αυτό αντιστοιχεί στο σχήμα της εκφώνησης. Η διάταξη που δίνει το μέγιστο δυνατό μήκος της άνω πολυγωνικής γραμμής είναι αυτή που φαίνεται στο σχήμα. Όπως αναφέραμε παραπάνω, η εν λόγω πολυγωνική γραμμή αποτελείται από τα ευθύγραμμα τμήματα DC, CG, GF, FJ, JI, IM, ML, LP, PO με συνολικό μήκος \(5 + 6 + 3 + 7 + 10 + 13 + 7 + 12 + 5 = 68\).
Subtasks
- Στο 35%, \(1 \leq N \leq 20\).
- Στο 65%, \(3 \leq N \leq 100.000\).