31ος ΠΔΠ Καμπ (seniors)
Αλλαγές ρίζας (rootit)
Δίνεται ένα δένδρο (συνεκτικό ακυκλικό γράφημα) με \(N\) κορυφές, αριθμημένες από το \(1\) έως το \(N\). Κάθε κορυφή του δένδρου έχει ένα θετικό ακέραιο βάρος. Συμβολίζουμε με \(W_i\) το βάρος της κορυφής \(i\). Θεωρούμε πως η ρίζα του δένδρου είναι αρχικά η κορυφή \(1\). Σε ένα τέτοιο δένδρο μπορούμε να εφαρμόσουμε δύο ειδών πράξεις:
- \(R\) \(r\) Αλλαγή της ρίζας του δέντρου, ώστε ρίζα να είναι τώρα η κορυφή \(r\).
- \(S\) \(u\) Ερώτημα: βρες το άθροισμα των βαρών των κορυφών που βρίσκονται στο υποδένδρο της κορυφής \(u\).
Αρχεία Εισόδου (rootit.in):
Στην πρώτη γραμμή της εισόδου θα δίνονται δύο θετικοί ακέραιοι \(N\), \(Q\): το πλήθος των κορυφών του δένδρου και το πλήθος των πράξεων που θα κληθούμε να εφαρμόσουμε. Στη δεύτερη γραμμή δίνονται \(N\) θετικοί ακέραιοι, ο \(i\)-οστός εκ τωνοστός εκ των οποίων είναι το βάρος του \(i\)-οστός εκ τωνοστού κόμβου \(W_i\) όπου \(1 \leq W_i \leq 10^6\). Στις επόμενες \(N−1\) γραμμές της εισόδου θα δίνεται η περιγραφή του δένδρου, σε κάθε γραμμή δηλαδή θα δίνονται \(2\) θετικοί ακέραιοι \(u\) και \(v\), από \(1\) μέχρι και \(N\), που εκφράζουν πως οι κόμβοι \(u\) και \(v\) συνδέονται με μία ακμή. Ακολουθούν Q γραμμές, κάθε μια εκ των οποίων είναι είτε της μορφής “R r” είτε της μορφής “S u”. Οι γραμμές αυτές παριστάνουν τις πράξεις που πρέπει να εφαρμόσουμε.
Σημείωση: Στην περίπτωση όπου έχουμε ερώτημα της μορφής “R r” δεν χρειάζεται να εκτυπώσουμε κάτι, απλώς εκτελούμε την αλλαγή της ρίζας του δέντρου
Αρχεία Εξόδου (rootit.out):
Για κάθε ερώτημα της μορφής “S u” που διαβάζουμε από την είσοδο, κατά σειρά, τυπώνουμε μία γραμμή που να περιέχει έναν θετικό ακέραιο αριθμό: το άθροισμα των βαρών που βρίσκονται στο υποδένδρο της κορυφής u με την υπάρχουσα μορφή του δέντρου.
Παράδειγμα Αρχείου Εισόδου - Εξόδου:
| rootit.in | rootit.out |
|---|---|
| 7 7 3 2 7 8 4 1 1 1 2 1 3 2 7 3 4 3 5 3 6 S 1 S 3 R 3 S 1 R 2 S 2 S 3 |
26 20 6 26 20 |
Εξήγηση παραδείγματος: Το διάνυσμα των βαρών των κορυφών του δένδρου είναι το εξής: \(W_1 = 3\), \(W_2 = 2\), \(W_3 = 7\), \(W_4 = 8\), \(W_5 = 4\), \(W_6 = 1\), \(W_7 = 1\).
Το δένδρο περνάει από τρεις φάσεις, την αρχική κατά την οποία η ρίζα είναι η κορυφή \(1\), μια δεύτερη στην οποία ρίζα γίνεται η κορυφή \(3\), και την τελική στην οποία ρίζα γίνεται η κορυφή \(2\). Οι τρεις αυτές φάσεις φαίνονται παρακάτω:
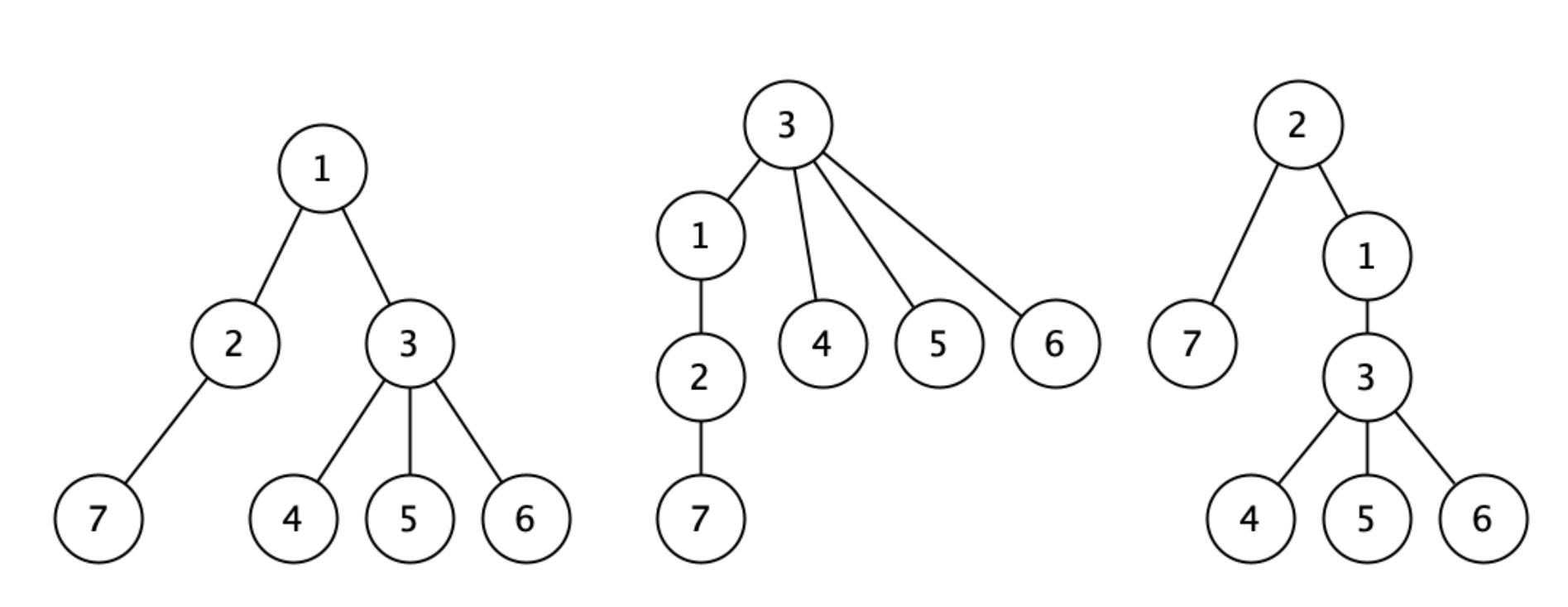
- Στην πρώτη πράξη (ερώτημα “S 1”) βρισκόμαστε στην πρώτη φάση με ρίζα την κορυφή \(1\) και η απάντηση είναι ίση με το βάρος όλων των κόμβων: \(W_1+W_2+W_3+W_4+W_5+W_6+W_7 = 3+2+7+8+4+1+1 = 26\).
- Στη δεύτερη πράξη (ερώτημα “S 3”) έχουμε ακόμα ρίζα την κορυφή \(1\) και συνεπώς η απάντηση είναι: \(W_3+W_4+W_5+W_6 = 7+8+4+1 = 20\).
- Στην τρίτη πράξη (αλλαγή ρίζας “R 3”) μεταβαίνουμε στη δεύτερη φάση με ρίζα την κορυφή \(3\).
- Στην τέταρτη πράξη (ερώτημα “S 1”) η απάντηση είναι \(W_1+W_2+W_7 = 3+2+1 = 6\).
- Στην πέμπτη πράξη (αλλαγή ρίζας “R 2”) μεταβαίνουμε στην τρίτη φάση με ρίζα την κορυφή \(2\).
- Στην έκτη πράξη (ερώτημα “S 2”) η απάντηση είναι \(W_1+W_2+W_3+W_4+W_5+W_6+W_7 = 3+2+7+8+4+1+1 = 26\).
- Στην έβδομη και τελευταία πράξη (ερώτημα “S 3”) η απάντηση είναι \(W_3+W_4+W_5+W_6 = 7+8+4+1 = 20\).
Subtasks
- Στο 20%, \(1 \leq N \leq 1.000\), \(1 \leq Q \leq 1.000\).
- Στο 30%, \(1 \leq N \leq 2.000\), \(1 \leq Q \leq 100.000\).
- Στο 50%, \(1 \leq N \leq 100.000\), \(1 \leq Q \leq 100.000\).