31ος ΠΔΠ Καμπ (seniors)
Διακοπές στη γραφούπολη (vacation)
Είμαστε στο έτος 7342 μ.Χ και η αγαπημένη μας δενδρούπολη βρίσκεται σε μεγάλη οικονομική ανάπτυξη. Έχουν κατασκευαστεί πολλοί δρόμοι μονής κυκλοφορίας, που από δένδρο την έχουν κάνει να μοιάζει με κατευθυνόμενο γράφο, γι’ αυτό και τώρα ονομάζεται γραφούπολη. Κάθε δρόμος που συνδέει δύο κορυφές \(u\) και \(v\) έχει ένα βάρος \(w\) που δηλώνει την απόσταση από την κορυφή \(u\) στην κορυφή \(v\). Πολλοί τουρίστες καταφθάνουν κάθε χρόνο στη γραφούπολη και εσείς, που έχετε ταξιδιωτικό γραφείο, θέλετε να αξιοποιήσετε αυτή την ευκαιρία. Θέλετε να οργανώσετε τους τουρίστες σε ομάδες τις οποίες θα ξεναγήσετε στη γραφούπολη.
Φέτος λοιπόν έχουν καταφθάσει ακριβώς \(T\) τουρίστες, οι οποίοι έχουν εγκατασταθεί στους κόμβους από \(1\) μέχρι \(T\). Θέλετε να χωρίσετε αυτούς τους τουρίστες σε \(K\) ομάδες. Εσείς βρίσκεστε στον κόμβο \(T+1\) και είστε ο υπεύθυνος επικοινωνίας του ταξιδιωτικού γραφείου. Αφού γίνει ο χωρισμός σε ομάδες, κάθε τουρίστας πρέπει να στείλει ένα μήνυμα σε όλους τους υπόλοιπους της ομάδας του. Προκειμένου ένας τουρίστας που βρίσκεται στην κορυφή u να στείλει μήνυμα στον τουρίστα που βρίσκεται στην κορυφή \(v\) πρέπει να ακολουθήσει την εξής διαδικασία: Αρχικά στέλνει μέσω ταχυδρομείου το μήνυμα σε εσάς (δηλαδή στην κορυφή \(T+1\)) και έπειτα εσείς, αφού το υπογράψετε, το στέλνετε πάλι μέσω ταχυδρομείου στην κορυφή \(v\). Επειδή όμως το ταχυδρομείο κοστίζει και θέλετε οι πελάτες σας να μείνουν ευχαριστημένοι, πρέπει να χωρίσετε κατάλληλα τους τουρίστες σε ομάδες ώστε η συνολική απόσταση που θα διανυθεί για να σταλούν όλα τα μηνύματα να είναι η ελάχιστη δυνατή.
Αρχεία Εισόδου (vacation.in):
Στην πρώτη γραμμή της εισόδου δίνονται τέσσερις θετικοί ακέραιοι αριθμοί \(N\), \(K\), \(T\), \(M\): το πλήθος των κορυφών της γραφούπολης, το πλήθος των ομάδων στις οποίες πρέπει να χωρίσετε τους τουρίστες, το πλήθος των τουριστών και το πλήθος των δρόμων μονής κατεύθυνσης της γραφούπολης, αντίστοιχα. Οι κορυφές είναι αριθμημένες από το \(1\) έως και το \(N\). Ακολουθούν \(M\) γραμμές (όπου \(1 \leq Μ \leq 50.000\)), καθεμία από τις οποίες περιγράφει έναν δρόμο και περιέχει τρεις ακεραίους \(u\), \(v\), \(w\): ο δρόμος από την κορυφή \(u\) στην κορυφή \(v\) έχει απόσταση \(w\) (όπου \(0 \leq w \leq 10.000\)). Υποθέστε ότι θα είναι \(1 \leq K \leq T < N\) και ότι θα υπάρχει πάντα τρόπος να σταλεί ένα μήνυμα από οποιονδήποτε τουρίστα προς εσάς και αντίστροφα.
Αρχεία Εξόδου (vacation.out):
Πρέπει να εκτυπώσετε μία γραμμή που να περιέχει έναν θετικό ακέραιο: την ελάχιστη συνολική απόσταση που θα διανύσουν όλα τα μηνύματα, στον βέλτιστο χωρισμό των τουριστών σε ομάδων.
Παράδειγμα Αρχείου Εισόδου - Εξόδου:
| vacation.in | vacation.out |
|---|---|
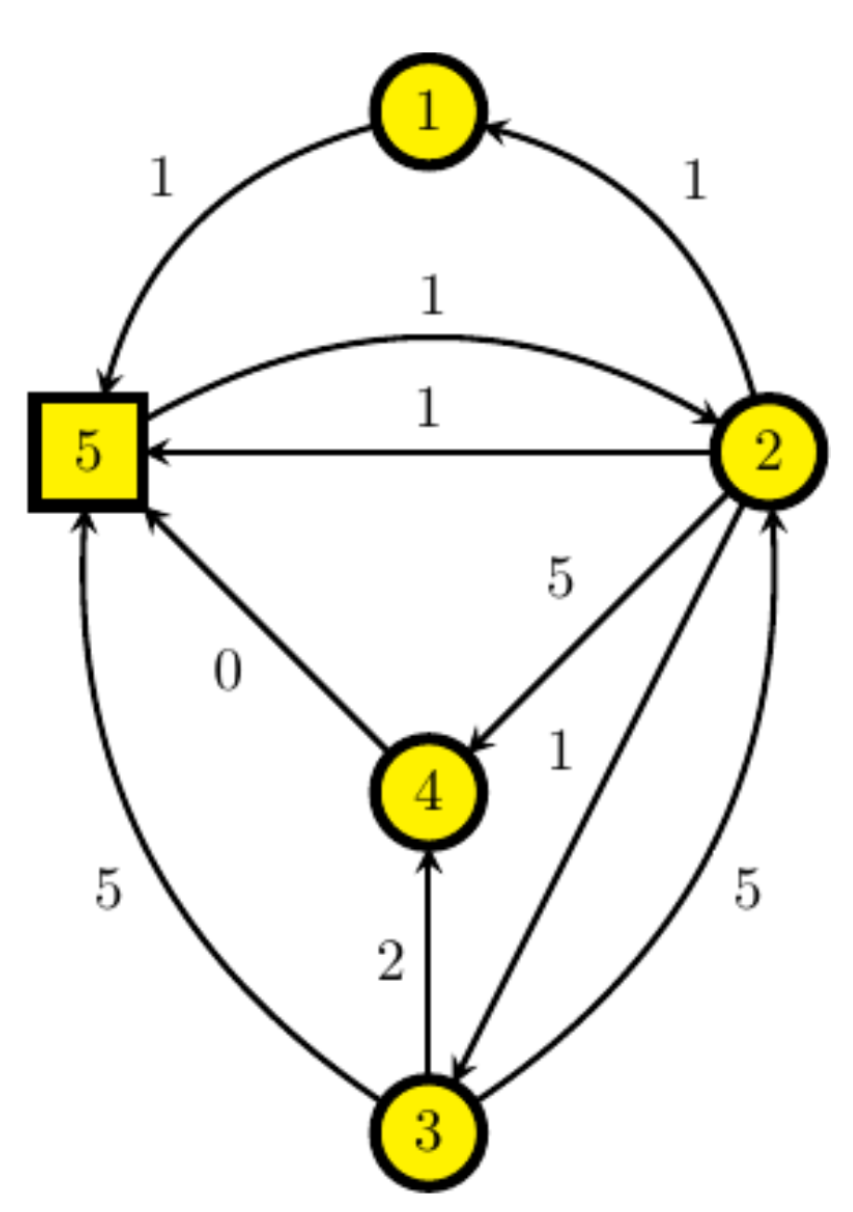
| 5 2 4 10 5 2 1 2 5 1 3 5 5 4 5 0 1 5 1 2 3 1 3 2 5 2 4 5 2 1 1 3 4 2 |
13 |
Εξήγηση παραδείγματος: Η μορφή της γραφούπολης φαίνεται στο διπλανό σχήμα. Οι τουρίστες βρίσκονται στις κορυφές \(1\) έως και \(4\) και εσείς βρίσκεστε στην κορυφή \(5\). Αν τοποθετήσετε τους τουρίστες \(1\) και \(2\) σε μία ομάδα και τους τουρίστες \(3\) και \(4\) σε μία δεύτερη ομάδα, τότε τα μηνύματα που θα πρέπει να σταλούν είναι:
- \(1 \to 2\): απόσταση \(1+1 = 2\)
- \(2 \to 1\): απόσταση \(1+2 = 3\)
- \(3 \to 4\): απόσταση \(2+4 = 6\)
- \(4 \to 3\): απόσταση \(0+2 = 2\) άρα συνολική απόσταση \(2+3+6+2 = 13\). Αυτή είναι και η ελάχιστη δυνατή.
Subtasks
- Στο 15%, \(3 \leq N \leq 5.000\), \(K = 1\).
- Στο 15%, \(3 \leq N \leq 20\), \(K = 2\).
- Στο 30%, \(3 \leq N \leq 250\), \(3 \leq K \leq 250\).
- Στο 40%, \(3 \leq N \leq 5.000\), \(3 \leq K \leq 5.000\).