32ος ΠΔΠ Γ' Φάση
Η τελευταία πίστα (supgame)

Παίζουμε ένα ηλεκτρονικό παιχνίδι που αποτελείται από \(Ν\) πίστες (επίπεδα δυσκολίας), αριθμημένες από \(1\) έως \(N\). Το παιχνίδι ξεκινάει υποχρεωτικά από την πίστα \(S\) και τερματίζεται μόλις φτάσουμε στην πίστα \(T\). Κάθε πίστα γενικά μπορεί να έχει πολλές εξόδους, που κάθε μία οδηγεί σε κάποια άλλη πίστα. Γνωρίζουμε όλες τις εξόδους και, για κάθε πίστα, έχουμε υπολογίσει πόσο χρόνο χρειαζόμαστε για να «κινηθούμε» μέσα σε αυτήν και να βγούμε από κάθε συγκεκριμένη έξοδό της. Ο χρόνος αυτός μπορεί να διαφέρει (δηλαδή, αν βρισκόμαστε στην πίστα \(1\), είναι πιθανό να χρειαζόμαστε \(3\) λεπτά για να βγούμε από την έξοδο που οδηγεί στην πίστα \(17\) και \(6\) λεπτά για να βγούμε από την έξοδο που οδηγεί στην πίστα \(42\)).

Στο παιχνίδι όμως υπάρχει ένας ακόμα περιορισμός. Υπάρχουν δύο συγκεκριμένες πίστες, η \(P\) και η \(Q\), και το παιχνίδι δε μας επιτρέπει να πάμε στην πίστα \(Q\) αν πρώτα δεν έχουμε πάει στην πίστα \(P\). Θέλουμε να ολοκληρώσουμε το παιχνίδι στον ελάχιστο δυνατό χρόνο. Δε χρειάζεται να τελειώσουμε όλες τις πίστες, αρκεί να φτάσουμε στην \(T\).

Πρόβλημα

Να αναπτύξετε ένα πρόγραμμα σε μια από τις γλώσσες της IOI (Pascal, C, C++, Java) το οποίο θα διαβάζει την περιγραφή των πιστών του παιχνιδιού και θα εκτυπώνει τον ελάχιστο δυνατό χρόνο στον οποίο μπορούμε να ολοκληρώσουμε το παιχνίδι.

Αρχεία εισόδου

Το αρχείο εισόδου με όνομα supgame.in είναι αρχείο κειμένου με την εξής δομή. Η πρώτη γραμμή του περιέχει έξι ακέραιους αριθμούς \(N, M, S, T, P, Q\), χωρισμένους ανά δύο με ένα κενό διάστημα: \(N\) είναι το πλήθος των πιστών, \(Μ\) είναι το συνολικό πλήθος των εξόδων που οδηγούν από μία πίστα σε μία άλλη, \(S\) και \(T\) είναι η αρχική και η τελική πίστα, \(P\) και \(Q\) είναι οι δύο πίστες που αναφέρει ο παραπάνω περιορισμός. Κάθε μία από τις επόμενες \(Μ\) γραμμές περιέχει τρεις ακέραιους αριθμους \(Χ_i\), \(Y_i\) και \(W_i\) χωρισμένους ανά δύο με ένα κενό διάστημα. Η τριάδα αυτή περιγράφει μία έξοδο: παίζοντας την πίστα \(Χ_i\) μπορούμε να βγούμε από την έξοδο \(Y_i\) σε χρόνο ίσο με \(W_i\) λεπτά. Θεωρήστε δεδομένο ότι θα είναι δυνατό να ολοκληρώσουμε το παιχνίδι.

Αρχεία εξόδου

Το αρχείο εξόδου με όνομα supgame.out είναι αρχείο κειμένου με την εξής δομή. Έχει ακριβώς μία γραμμή που περιέχει ακριβώς έναν ακέραιο αριθμό: τον ελάχιστο χρόνο, σε λεπτά, που απαιτείται για την ολοκλήρωση του παιχνιδιού.

1^o

supgame.in	supgame.out
6 9 1 6 2 4 1 2 2 2 3 2 1 3 3 3 4 10 3 5 8 4 5 3 5 4 5 4 6 3 5 6 12	17

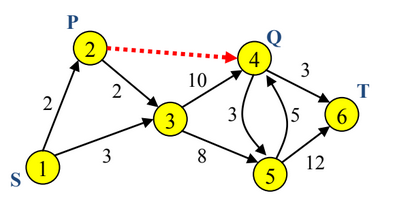
Εξήγηση: Το παιχνίδι αντιστοιχεί στο παρακάτω σχήμα. Μπορούμε να παίξουμε τις πίστες με την εξής σειρά: \(1, 2, 3, 4, 6\). Θα χρειαστούμε \(2+2+10+3=17\) λεπτά. Ο περιορισμός ικανοποιείται, γιατί όταν φτάνουμε στην πίστα \(4\) έχουμε ήδη περάσει από την πίστα \(2\). Δεν είναι δυνατό να τα καταφέρουμε σε λιγότερα από \(17\) λεπτά.

Περιορισμοί

• Ισχύει \(2 \le N \le 60.000, 1 \le M \le 200.000\)
• Ισχύει \(1 \le S \le N, 1 \le T \le N, S \ne T\)
• Ισχύει \(1 \le P \le N, 1 \le Q \le N, P \ne Q\)
• Ισχύει \(1 \le X_i \le N, 1 \le Y_i \le N, X_i \ne Y_i\)
• Ισχύει \(1 \le W_i \le 50.000\)
• Για περιπτώσεις ελέγχου συνολικής αξίας 30%, η βέλτιστη διαδρομή από την πίστα \(S\) προς την πίστα \(T\) δε θα περνάει από την πίστα \(Q\).

Προσοχή! Φροντίστε να διαβάζετε την είσοδο και να εκτυπώνετε την έξοδο αποδοτικά, ειδικά αν προγραμματίζετε σε C++ ή Java.

Παρατηρήσεις:

• Μορφοποίηση: Στην έξοδο, όλες οι γραμμές τερματίζουν με ένα χαρακτήρα newline.
• Μέγιστος χρόνος εκτέλεσης: \(1\) sec.
• Μέγιστη διαθέσιμη μνήμη: \(256\) MB.