32ος ΠΔΠ Καμπ (κοινά)
Να προλάβουμε το πάρτυ! (shortcuts)

Μας δίνεται το οδικό δίκτυο της χώρας. Υπάρχουν \(N\) πόλεις (αριθμημένες από \(1\) μέχρι \(N\)) και \(M\) δρόμοι μονής κατεύθυνσης που συνδέουν ζεύγη διαφορετικών πόλεων. Για κάθε δρόμο γνωρίζουμε το χρόνο (σε ώρες) που χρειάζεται για να ταξιδέψουμε από το ένα άκρο του στο άλλο. Θέλουμε να πάμε από την πόλη \(S\), όπου μένουμε, στην πόλη \(T\), όπου κάνει πάρτυ ο καλύτερος φίλος μας. Βλέπουμε όμως με μεγάλη μας λύπη ότι δεν προλαβαίνουμε να φτάσουμε εκεί πριν το πάρτυ, που θα γίνει σε \(B\) ώρες! Δε θέλουμε με τίποτα να χάσουμε το πάρτυ!

Για καλή μας τύχη, εμφανίζεται η καλή νεράιδα. Αυτή μάς προτείνει την εξής συμφωνία: θα της δώσουμε ένα υποσύνολο των δρόμων και εκείνη θα κάνει τα μαγικά της έτσι ώστε αυτούς τους δρόμους να μπορούμε να τους ταξιδέψουμε σε μηδενικό χρόνο! Όμως, για κάθε ένα δρόμο που «μηδενίζει» η νεράιδα, εμείς θα πρέπει να κάνουμε μία καλή πράξη (π.χ., να βοηθήσουμε για ένα χρόνο στη διεξαγωγή του camp του ΠΔΠ όταν τελειώσουμε το σχολείο!) κι εμείς δε θέλουμε να δεσμευτούμε ότι θα κάνουμε πολλές καλές πράξεις!

Βρείτε τον ελάχιστο αριθμό δρόμων που θα ζητήσετε να «μηδενίσει» η νεράιδα, έτσι ώστε να προλάβετε το πάρτυ του φίλου σας!

Αρχεία Εισόδου (shortcuts.in):

Η πρώτη γραμμή της εισόδου θα περιέχει πέντε φυσικούς αριθμούς \(N\), \(M\), \(S\), \(T\) και \(B\), χωρισμένους ανά δύο με ένα κενό διάστημα: το πλήθος των πόλεων, το πλήθος των δρόμων, την πόλη αφετηρία και την πόλη προορισμό, και το πλήθος των ωρών που έχουμε στη διάθεσή μας πριν το πάρτυ του φίλου μας.

Κάθε μία από τις επόμενες \(M\) γραμμές περιγράφει έναν δρόμο μονής κατεύθυνσης. Περιέχει τρεις ακέραιους αριθμούς \(U_i\), \(V_i\) και \(T_i\), χωρισμένους ανά δύο με ένα κενό διάστημα. Μία τέτοια γραμμή σημαίνει ότι μπορούμε να πάμε από την πόλη \(U_i\) στην πόλη \(V_i\) και το ταξίδι αυτό θα διαρκέσει \(T_i\) ώρες.

Θεωρήστε ότι θα είναι πάντοτε εφικτό να ταξιδέψετε από την πόλη \(S\) στην πόλη \(T\).

Αρχεία Εξόδου (shortcuts.out):

Η έξοδος πρέπει να περιέχει μία γραμμή με ακριβώς έναν ακέραιο αριθμό: το ελάχιστο δυνατό πλήθος δρόμων που θα ζητήσουμε στη νεράιδα να μας «μηδενίσει» για να προλάβουμε το πάρτυ του φίλου μας.

Παράδειγμα Αρχείου Εισόδου - Εξόδου:

shortcuts.in	shortcuts.out
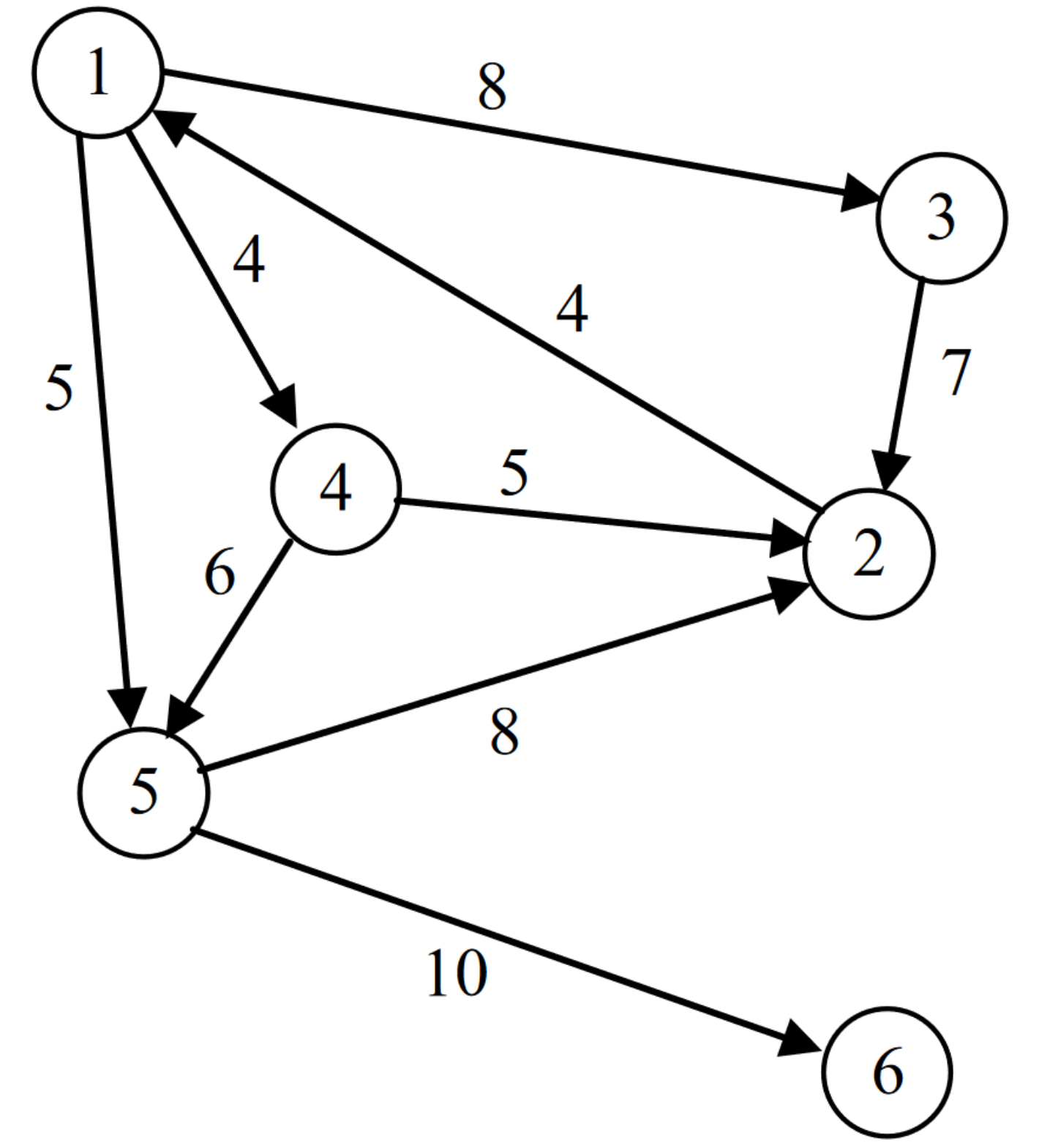
6 9 3 6 15 2 1 4 3 2 7 4 5 6 1 3 8 1 4 4 5 2 8 5 6 10 1 5 5 4 2 5	2

Εξήγηση παραδείγματος: Θέλουμε να πάμε από την πόλη \(3\) στην πόλη \(6\) και έχουμε \(15\) ώρες στη διάθεσή μας. Αν ζητήσουμε από τη νεράιδα να «μηδενίσει» τους δρόμους \(3 \to 2\) και \(2 \to 1\), τότε μπορούμε να φτάσουμε ακριβώς σε \(15\) ώρες. Δεν υπάρχει τρόπος να τα καταφέρουμε μηδενίζοντας λιγότερους από δύο δρόμους.

Περιορισμοί:

\(1 \leq N \leq 1.000\).
\(1 \leq Μ \leq 10.000\).
\(1 \leq B \leq 1.000.000.000\).
\(1 \leq S \leq N\), \(1 \leq T \leq N\), \(S \neq T\).
\(1 \leq U_i \leq N\), \(1 \leq V_i \leq N\), \(U_i \neq V_i\).
\(1 \leq T_i \leq 2.000.000\).
Δε θα δίνονται περισσότεροι από ένας δρόμοι με τα ίδια άκρα και την ίδια κατεύθυνση.
Το άθροισμα όλων των \(T_i\) δε θα υπερβαίνει το \(1.000.000.000\).
Όριο χρόνου εκτέλεσης: \(1\) sec.
Όριο μνήμης: \(256\) MB.

Subtasks