35ος ΠΔΠ B' Φάση Λυκείου
Επισκευή δρόμου (roadfix)
Σε έναν επαρχιακό δρόμο πρόκειται να γίνει ένας αγώνας σκυταλοδρομίας (ίσως αυτός του προβλήματος της Β’ φάσης του γυμνασίου, που όμως δε χρειάζεται να διαβάσετε για να λύσετε αυτό το πρόβλημα). Ο δρόμος όμως έχει τα κακά του τα χάλια, το οδόστρωμα έχει φθαρεί και χρειάζεται άμεσα επισκευή. Ο δήμαρχος κάνει αμέσως διαγωνισμό για την επισκευή και μαζεύει προσφορές από συνεργεία που προτίθενται να επισκευάσουν τμήματα του δρόμου. Κάθε προσφορά είναι μία τριάδα \((X_i, L_i, C_i)\) που σημαίνει ότι κάποιο συνεργείο προτίθεται να επισκευάσει το τμήμα του δρόμου που αρχίζει στο χιλιόμετρο \(X_i\) και έχει μήκος \(L_i\) χιλιόμετρα, με κόστος \(C_i\).
Βοηθήστε τον δήμαρχο να βρει το ελάχιστο κόστος που απαιτείται για να επισκευάσει οποιοδήποτε τμήμα του δρόμου. Προσέξτε ότι για να επισκευαστεί ένα τμήμα του δρόμου που αρχίζει στο χιλιόμετρο \(Y_j\) και έχει μήκος \(K_j\) χιλιόμετρα, o δήμαρχος πρέπει να επιλέξει ένα υποσύνολο των προσφορών που συνολικά να καλύπτουν όλο αυτό το τμήμα του δρόμου. Ενδέχεται κάποια μέρη του τμήματος αυτού να καλύπτονται από περισσότερες από μία προσφορές. Επίσης, ενδέχεται κάποιες από τις προσφορές που θα επιλέξει να επισκευάζουν και μέρη του δρόμου εκτός του εν λόγω τμήματος.
Πρόβλημα
Να αναπτύξετε ένα πρόγραμμα σε μια από τις γλώσσες του IOI (PASCAL, C, C++, Java) το οποίο θα διαβάζει τις προσφορές για την επισκευή τμημάτων του δρόμου και θα απαντά σε έναν αριθμό ερωτημάτων της μορφής: ποιο είναι το ελάχιστο κόστος για την επισκευή κάποιου συγκεκριμένου τμήματος του δρόμου. Κάθε ερώτημα πρέπει να απαντάται ανεξάρτητα από τα υπόλοιπα ερωτήματα.
Αρχεία Εισόδου:
Τα αρχεία εισόδου με όνομα roadfix.in είναι αρχεία κειμένου με την εξής δομή: Η πρώτη γραμμή της εισόδου θα περιέχει δύο φυσικούς αριθμούς \(N, M\), χωρισμένους με ένα κενό διάστημα: το πλήθος των προσφορών και το πλήθος των ερωτημάτων που θα γίνουν.
Κάθε μία από τις επόμενες \(N\) γραμμές περιγράφει μία προσφορά: περιέχει τρεις ακέραιους αριθμούς \(X_i\), \(L_i\) και \(C_i\), χωρισμένους ανά δύο με ένα κενό διάστημα.
Κάθε μία από τις επόμενες \(M\) γραμμές περιγράφει ένα ερώτημα: περιέχει δύο ακέραιους αριθμούς \(Y_j\) και \(K_j\), χωρισμένους μεταξύ τους με ένα κενό διάστημα.
Αρχεία Εξόδου:
Τα αρχεία εξόδου με όνομα roadfix.out είναι αρχεία κειμένου με την εξής δομή. Περιέχουν ακριβώς \(M\) γραμμές που κάθε μία περιέχει έναν ακέραιο αριθμό: το ελάχιστο κόστος για την επισκευή του τμήματος του δρόμου του αντίστοιχου ερωτήματος, κατά σειρά. Αν η επισκευή του τμήματος δεν είναι εφικτή, η γραμμή που αντιστοιχεί στο ερώτημα πρέπει να περιέχει τον αριθμό \(−1\).
Περιορισμοί:
- \(2 \leq N \leq 10.000\),
- \(1 \leq M \leq 10\),
- \(1 \leq X_i < X_i+L_i \leq 1.000.000.000\),
- \(1 \leq C_i \leq 10.000\),
- \(1 \leq Y_j < Y_j+K_j \leq 1.000.000.000\).
Παράδειγμα Αρχείων Εισόδου - Εξόδου:
| roadfix.in | roadfix.out |
|---|---|
| 5 3 30 45 20 40 40 30 60 35 5 20 25 10 90 10 15 20 80 50 30 10 30 |
50 25 -1 |
Εξήγηση:
Υπάρχουν πέντε προσφορές, οι οποίες καλύπτουν τα τμήματα του δρόμου που φαίνονται στο παρακάτω σχήμα.
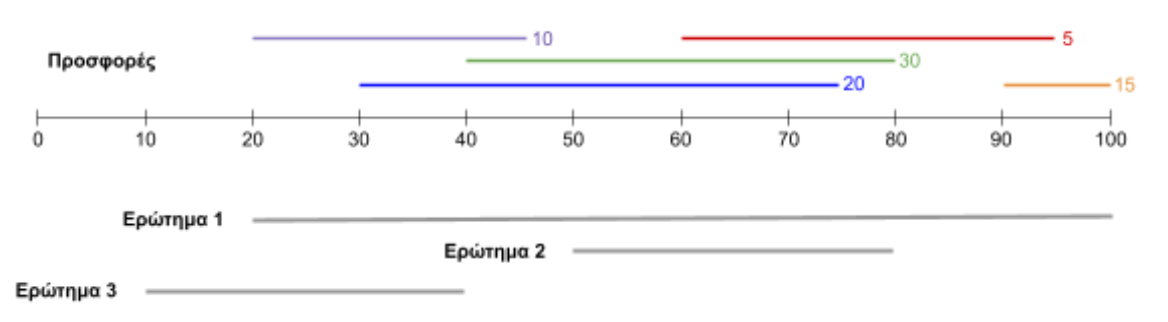
Για το πρώτο ερώτημα, το τμήμα του δρόμου από το \(20\) μέχρι το \(100\) (μήκους \(80\)) μπορεί να επισκευαστεί με το ελάχιστο κόστος επιλέγοντας τις προσφορές \(10+20+5+15 = 50\). (Επιλέγοντας την προσφορά \(30\) αντί της \(20\) θα πετυχαίναμε επίσης το ζητούμενο αλλά με μεγαλύτερο συνολικό κόστος.) Για το δεύτερο ερώτημα, το ελάχιστο κόστος είναι \(20+5=25\). Για το τρίτο ερώτημα, το τμήμα του δρόμου από το \(10\) μέχρι το \(20\) δεν επισκευάζεται με καμία από τις προσφορές, άρα η απάντηση είναι \(−1\).
Παρατηρήσεις:
Μορφοποίηση: Στην είσοδο αλλά και στην έξοδο, κάθε γραμμή τερματίζει με έναν χαρακτήρα newline.
Μέγιστος χρόνος εκτέλεσης: \(1\) sec.
Μέγιστη διαθέσιμη μνήμη: \(64\) MB.