36ος ΠΔΠ B' Φάση Λυκείου
Η δημόσια βιβλιοθήκη (publib)
Επεξήγηση εκφώνησης
Μας δίνεται ένας μη-κατευθυνόμενος γράφος και μας ζητείται να βρούμε την ακτίνα του γράφου.
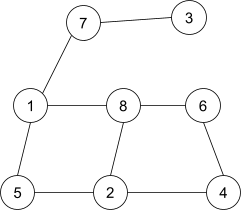
Στο παράδειγμα της εκφώνησης, ο κόμβος \(1\) απέχει \(2\) από τον κόμβο \(2\), απέχει \(2\) από τον κόμβο \(3\), απέχει \(3\) από τον κόμβο \(4\), κ.ο.κ. Συνοψίζοντας μπορούμε να βάλουμε τις αποστάσεις στην παρακάτω γραμμή:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | 2 | 2 | 3 | 1 | 2 | 1 | 1 |
Παρατηρήστε ότι η μέγιστη απόσταση από τον κόμβο \(1\) είναι προς τον κόμβο \(4\). Επαναλαμβάνοντας για τους υπόλοιπους κόμβους, έχουμε
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0 | 2 | 2 | 3 | 1 | 2 | 1 | 1 |
| 2 | 2 | 0 | 4 | 1 | 1 | 2 | 3 | 1 |
| 3 | 2 | 4 | 0 | 5 | 3 | 4 | 1 | 3 |
| 4 | 3 | 1 | 5 | 0 | 2 | 1 | 4 | 2 |
| 5 | 1 | 1 | 3 | 2 | 0 | 3 | 2 | 2 |
| 6 | 2 | 2 | 4 | 1 | 3 | 0 | 3 | 1 |
| 7 | 1 | 3 | 1 | 4 | 2 | 3 | 0 | 2 |
| 8 | 1 | 1 | 3 | 2 | 2 | 1 | 2 | 0 |
όπου με έντονα γράμματα αποτυπώνεται η μέγιστη απόσταση για κάθε κόμβο. Η μικρότερη από αυτές είναι η απάντηση, δηλαδή η ακτίνα του γράφου, και δίνεται με κόκκινο. Υπάρχουν τρεις κόμβοι που πετυχαίνουν αυτή την ελάχιστη απόσταση, ο \(1\), ο \(5\) και ο \(8\).
Βέλτιστη λύση
Σε έναν μη-κατευθυνόμενο γράφο όπου οι ακμές δεν έχουν βάρη μπορούμε να βρούμε την συντομότερη απόσταση από έναν κόμβο \(u\) προς όλους τους άλλους χρησιμοποιώντας την αναζήτηση κατά πλάτος (ή αλλιώς BFS). Ο τρόπος που δουλεύει ο αλγόριθμος είναι ο εξής:
- Ξεκινάμε με μία ουρά (queue) που αρχικά έχει τον κόμβο \(u\) (με απόσταση \(0\))
- Κατόπιν επαναλαμβάνουμε όσο η ουρά δεν έχει αδειάσει:
- Αφαιρούμε κάθε κόμβο και την απόσταση του \(d\) από την ουρά, και προσθέτουμε στο τέλος της ουράς με απόσταση \(d+1\), τους γείτονες του που δεν έχουμε ήδη συναντήσει.
Ο τελευταίος κόμβος που προσθέτουμε έχει τη μέγιστη απόσταση από τον κόμβο \(u\). Επομένως, επαναλαμβάνουμε την αναζήτηση κατά πλάτος μία φορά από κάθε κόμβο, και η ελάχιστη μέγιστη απόσταση είναι η ακτίνα του γράφου. Ο παρακάτω κώδικας υλοποιεί ακριβώς αυτό.
std::vector<bool> visited(N); // Αν έχουμε επισκεφτεί έναν κόμβο.
std::queue<std::pair<long, long>> q; // Η ουρά.
std::fill(visited.begin(), visited.end(), false);
q.push({ i, 0 });
visited[i] = true;
long max_dist = 0;
// Τρέχουμε την BFS.
while (!q.empty()) {
auto [v, d] = q.front();
q.pop();
for (auto neigh : adj[v]) {
if (!visited[neigh]) {
q.push({neigh, d + 1});
visited[neigh] = true;
}
}
max_dist = d;
}
graph_radius = std::min(max_dist, graph_radius);
}
Παρακάτω δίνεται ένα παράδειγμα εκτέλεσης της αναζήτησης κατά πλάτος για τον κόμβο \(u = 1\), όπου η ουρά \(q\) κρατάει τα ζεύγη κόμβου και απόστασης:
Κάθε αναζήτηση κατά πλάτος θέλει \(\mathcal{O}(M)\) χρόνο, επομένως συνολικά ο αλγόριθμος χρειάζεται \(O(N \cdot M)\) χρόνο. Μπορείτε να βρείτε ολόκληρο τον κώδικα εδώ.
Εναλλακτικές υλοποιήσεις: Η ουρά μπορεί να υλοποιηθεί με την χρήση ενός πίνακα, που ενώ έχει την ίδια πολυπλοκότητα, στην πράξη είναι λίγο πιο γρήγορη γιατί αποφεύγει τις πολλές δεσμεύσεις μνήμης (δείτε εδώ τον κώδικα). Επίσης, η αναζήτηση κατά πλάτος, μπορεί να υλοποιηθεί με δύο πίνακες ακεραίων αντί για μία ουρά με ζεύγη (δείτε εδώ τον κώδικα).