36ος ΠΔΠ Καμπ (κοινά)
flood (flood)

Δίνεται ένα σύστημα $N$ δεξαμενών νερού, που συνδέονται μεταξύ τους με $M$ σωλήνες. Κάθε δεξαμενή είναι αριθμημένη με έναν αριθμό $i$ (όπου $1 \leq i \leq N$) και έχει μία γνωστή χωρητικότητα $C_i$ — δηλαδή πόσες μονάδες νερού χωράει. Κάθε σωλήνας συνδέει δύο δεξαμενές που βρίσκονται σε διαφορετικό ύψος και, μέσα σε αυτόν, το νερό κινείται από τη δεξαμενή που βρίσκεται ψηλότερα προς τη δεξαμενή που βρίσκεται χαμηλότερα (ποτέ αντίστροφα).

Όταν μια δεξαμενή υπερχειλίσει, το περίσσευμα νερού κατευθύνεται μέσω των σωλήνων προς τις χαμηλότερες δεξαμενές με τις οποίες αυτή συνδέεται. Αν υπάρχουν περισσότεροι σωλήνες που συνδέουν τη δεξαμενή με άλλες χαμηλότερες δεξαμενές, ο τρόπος που μοιράζεται το περίσσευμα νερού είναι ο εξής. Οι χαμηλότερες δεξαμενές ταξινομούνται βάσει του αριθμού τους σε αύξουσα σειρά. Η πρώτη μονάδα περισσευούμενου νερού πηγαίνει στην πρώτη κατά σειρά δεξαμενή, η δεύτερη στη δεύτερη, κ.ο.κ. Αν το περισσευούμενο νερό είναι περισσότερο από τις δεξαμενές, η διαδικασία αυτή επαναλαμβάνεται από την αρχή μέχρι να τελειώσει το περισσευούμενο νερό.

Αν όμως μια δεξαμενή υπερχειλίσει και δεν υπάρχει κανένας σωλήνας που να τη συνδέει με άλλη χαμηλότερη δεξαμενή, τότε το σύστημα πλημμυρίζει. Αυτό πρέπει να αποφευχθεί. Σε αυτό το πρόβλημα θα πρέπει να απαντήσετε $Q$ ερωτήματα για το ίδιο σύστημα δεξαμενών νερού. Κάθε ερώτηση $j$ (όπου $1 \leq j \leq Q$) θα είναι ανεξάρτητη από τις άλλες και θα έχει τη μορφή:

Αν όλες οι δεξαμενές είναι αρχικά άδειες, ποια είναι η μέγιστη ποσότητα νερού που μπορώ να ρίξω στη δεξαμενή $S_j$ χωρίς να πλημμυρίσει το σύστημα;

Δεδομένα εισόδου (flood.in)

Η πρώτη γραμμή της εισόδου θα περιέχει τρεις ακεραίους αριθμούς $N$, $M$ και $Q$, χωρισμένους ανά δύο με ένα κενό διάστημα: το πλήθος των δεξαμενών, το πλήθος των σωλήνων και το πλήθος των ερωτημάτων προς απάντηση. Η δεύτερη γραμμή θα περιέχει $N$ αριθμούς χωρισμένους ανά δύο με ένα κενό διάστημα: τις χωρητικότητες $C_i$ των δεξαμενών. Κάθε μία από τις επόμενες $M$ γραμμές θα περιέχει δύο αριθμούς $U$ και $V$, χωρισμένους με ένα κενό διάστημα: αυτό σημαίνει ότι υπάρχει ένας σωλήνας που κατευθύνεται από τη δεξαμενή $U$ (που βρίσκεται ψηλότερα) προς τη δεξαμενή $V$ (που βρίσκεται χαμηλότερα). Η τελευταία γραμμή της εισόδου θα περιέχει $Q$ αριθμούς, χωρισμένους ανά δύο με ένα κενό διάστημα: τις αρχικές δεξαμενές $S_j$ των ερωτημάτων που πρέπει να απαντηθούν.

Δεδομένα εξόδου (flood.out)

Η έξοδος πρέπει να αποτελείται από $Q$ γραμμές που κάθε μία να περιέχει ακριβώς έναν ακέραιο αριθμό: την απάντηση στο αντίστοιχο ερώτημα, κατά σειρά.

Παραδείγματα αρχείων εισόδου-εξόδου:

1^o

flood.in	flood.out
9 10 7 5 3 1 7 9 5 19 2 4 1 2 2 3 3 7 4 5 4 8 1 4 8 9 4 3 4 6 5 7 1 2 3 4 5 6 8	44 23 20 29 28 5 6

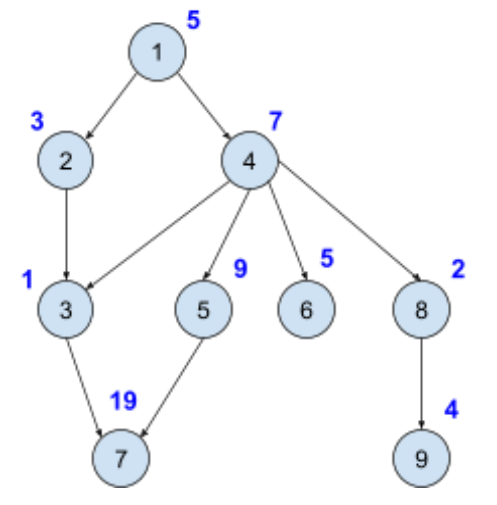
Εξήγηση: Το σύστημα των δεξαμενών φαίνεται στο σχήμα παραπάνω, όπου οι κύκλοι παριστάνουν τις δεξαμενές. Στο εσωτερικό κάθε κύκλου είναι γραμμένος ο αριθμός της δεξαμενής, ενώ εξωτερικά είναι γραμμένη η χωρητικότητά της. Για το πρώτο ερώτημα, αν ρίξουμε $44$ μονάδες νερού στη δεξαμενή $1$ (την ψηλότερη όλων) τότε θα συμβούν τα εξής:

Η δεξαμενή $1$ δέχεται $44$ μονάδες νερού και έχει χωρητικότητα $5$, άρα $39$ μονάδες νερού θα υπερχειλίσουν. Από αυτές, $20$ θα πάνε στη δεξαμενή $2$ και $19$ στη δεξαμενή $4$.
Η δεξαμενή $2$ δέχεται $20$ μονάδες νερού και έχει χωρητικότητα $3$, άρα $17$ μονάδες θα νερού θα υπερχειλίσουν και θα πάνε στη δεξαμενή $3$.
Η δεξαμενή $4$ δέχεται $19$ μονάδες νερού και έχει χωρητικότητα $7$, άρα $12$ μονάδες νερού θα υπερχειλίσουν. Θα πάνε στις δεξαμενές $3$, $5$, $6$ και $8$, που θα πάρουν από $3$ μονάδες κάθε μία.
Η δεξαμενή $8$ δέχεται $3$ μονάδες νερού και έχει χωρητικότητα $2$, άρα μία μονάδα θα υπερχειλίσει και θα πάει στην δεξαμενή $9$.
Η δεξαμενή $9$ δέχεται $1$ μονάδα νερού και έχει χωρητικότητα $4$, άρα δε θα υπερχειλίσει.
Οι δεξαμενές $5$ και $6$ δέχονται $3$ μονάδες νερού και έχουν χωρητικότητες αντίστοιχα $9$ και $5$, άρα δε θα υπερχειλίσουν.
Η δεξαμενή $3$ δέχεται συνολικά $20$ μονάδες νερού: $17$ από τη δεξαμενή $2$ και $3$ από τη δεξαμενή $4$. Έχει χωρητικότητα $1$, άρα $19$ μονάδες θα υπερχειλίσουν και θα πάνε στη δεξαμενή $7$.
Η δεξαμενή $7$ δέχεται $19$ μονάδες νερού και έχει χωρητικότητα $19$, άρα δε θα υπερχειλίσει.

Επομένως, ρίχνοντας $44$ μονάδες νερού στη δεξαμενή $1$ το σύστημα δεν πλημμυρίζει. Αν όμως βάλουμε έστω και μια μονάδα νερού παραπάνω, αυτό θα έχει ως αποτέλεσμα η δεξαμενή $7$ να δεχθεί περισσότερες από $19$ μονάδες νερού, με αποτέλεσμα να πλημμυρίσει το σύστημα.

Προσέξτε ότι αν αλλάξουμε την αρίθμηση των δεξαμενών στο παραπάνω σύστημα και κάνουμε ακριβώς τα ίδια ερωτήματα, οι απαντήσεις μπορεί να είναι διαφορετικές, λόγω του τρόπου διαμερισμού του περισσευούμενου νερού σε περίπτωση υπερχείλισης μιας δεξαμενής.

2^o

flood.in	flood.out
9 10 7 19 7 5 2 5 9 1 3 4 6 1 8 7 2 4 2 7 2 6 3 8 2 5 4 9 7 1 3 2 3 8 7 2 6 5 4	46 23 20 28 28 5 6

Εξήγηση: Αυτό το παράδειγμα είναι το ίδιο με το πρώτο, αλλά με διαφορετική αρίθμηση των δεξαμενών.

Περιορισμοί:

$1 \leq N \leq 2.000$,
$1 \leq M \leq 100.000$,
$1 \leq Q \leq 2.000$,
$1 \leq C_i \leq 10^9$.
Κάθε σωλήνας θα συνδέει δύο διαφορετικές έγκυρες δεξαμενές, που η πρώτη βρίσκεται ψηλότερα από τη δεύτερη. (Δηλαδή, θα είναι δυνατό σε κάθε δεξαμενή να αντιστοιχιστεί ένα ύψος με τέτοιο τρόπο ώστε όλοι οι σωλήνες να είναι συνεπείς.) Δε θα δίνεται ο ίδιος σωλήνας περισσότερες φορές.

Προσέξτε ότι για μεγάλες τιμές των $N$ και $C_i$ η απάντηση στα ερωτήματα μπορεί να υπερβαίνει το $2^{32}$.

Subtasks

Για περιπτώσεις ελέγχου συνολικής αξίας 23% θα είναι $Q \leq 10$ και κανείς αριθμός στο αρχείο εισόδου δε θα υπερβαίνει το 100.
Για περιπτώσεις ελέγχου συνολικής αξίας 47% σε κάθε δεξαμενή θα καταλήγει το πολύ ένας σωλήνας.