36ος ΠΔΠ Καμπ (seniors)
rotation (rotation)

Σε έναν κύκλο είναι τοποθετημένα \(T\) χρωματιστά φώτα, συμμετρικά σε ίσες αποστάσεις μεταξύ τους στην περιφέρεια του κύκλου. Κάθε φως έχει διαφορετικό χρώμα και μπορεί να είναι αναμμένο ή σβηστό. Γνωρίζουμε ακριβώς ποια φώτα είναι αναμμένα και ποια είναι σβηστά.

Αν περιστρέψουμε δεξιόστροφα τον κύκλο κατά μία γωνία \(\phi = 2\pi/T\), κάθε φως θα μετακινηθεί στη θέση του αμέσως δεξιότερου από αυτό. Η εικόνα των χρωματιστών φώτων που προκύπτει έτσι είναι διαφορετική από την αρχική, αφού είπαμε ότι τα φώτα έχουν διαφορετικά χρώματα. Έτσι, περιστρέφοντας τον κύκλο διαδοχικά για γωνίες \(\phi\) που είναι πολλαπλάσια του \(\phi = 2\pi/T\), μπορούμε να σχηματίσουμε συνολικά \(T\) διαφορετικές μεταξύ τους εικόνες (μαζί με την αρχική).

Ο σκύλος μου ο Αζώρ έχει αχρωματοψία. Για αυτόν, όλα τα χρώματα φαίνονται ίδια και μόνο τα αναμμένα ή τα σβηστά φώτα κάνουν διαφορά. Πόσες διαφορετικές εικόνες των φώτων βλέπει ο Αζώρ;

Δεδομένα εισόδου (rotation.in)

Στην πρώτη γραμμή της εισόδου θα υπάρχουν δύο θετικοί ακέραιοι, \(N\) και \(T\), το πλήθος των φώτων που είναι αναμμένα και το συνολικό πλήθος των φώτων, αντίστοιχα. Θεωρήστε ότι τα φώτα είναι αριθμημένα από το \(0\) μέχρι το \(T−1\).

Η δεύτερη γραμμή θα περιέχει ακριβώς \(N\) ακέραιους ακεραίους \(A_1, A_2, \ldots, A_N\), χωρισμένους ανά δύο με ένα κενό διάστημα: τους αριθμούς των φώτων που είναι αναμμένα στην αρχική θέση.

Στα παραδείγματα που ακολουθούν κάνουμε την αυθαίρετη παραδοχή ότι το φως \(0\) είναι αυτό που βρίσκεται στην βορειότερη θέση του κύκλου και ότι τα υπόλοιπα είναι αριθμημένα σε αύξουσα σειρά, σύμφωνα με τη φορά των δεικτών του ρολογιού.

Δεδομένα εξόδου (rotation.out)

Η έξοδος θα πρέπει να περιέχει μία γραμμή με έναν ακέραιο αριθμό: το πλήθος των διαφορετικών εικόνων που βλέπει ο Αζώρ αν περιστρέψουμε τον κύκλο όπως περιγράφηκε παραπάνω.

Παραδείγματα αρχείων εισόδου-εξόδου:

1^o

rotation.in	rotation.out
2 5 1 3	5

Εξήγηση: Σε αυτό το παράδειγμα είναι \(T=5\) και στην αρχική θέση είναι αναμμένα μόνο δύο φώτα. Μαζί με την αρχική, υπάρχουν πέντε εικόνες που προκύπτουν από την περιστροφή των φώτων, για \(\phi \in \{ 0, 2\pi/5, 4\pi/5, 6\pi/5, 8\pi/5 \}\), όπως δείχνει το παρακάτω σχήμα. Όλες οι εικόνες φαίνονται διαφορετικές στον Αζώρ.

2^o

rotation.in	rotation.out
2 4 1 3	2

Εξήγηση: Σε αυτό το παράδειγμα είναι \(T=4\) και στην αρχική θέση είναι αναμμένα πάλι μόνο δύο φώτα. Μαζί με την αρχική, υπάρχουν τέσσερις εικόνες που προκύπτουν από την περιστροφή των φώτων, όπως φαίνεται παρακάτω. Όμως, για τον Αζωρ που έχει αχρωματοψία, η εικόνα που προκύπτει όταν \(\phi = \pi\) φαίνεται ίδια με την αρχική εικόνα. Επίσης, η εικόνα που προκύπτει όταν \(\phi = 3\pi/2\) φαίνεται ίδια με εκείνη που προκύπτει όταν \(\phi = \pi/2\). Επομένως, ο Αζώρ βλέπει μόνο δύο διαφορετικές εικόνες.

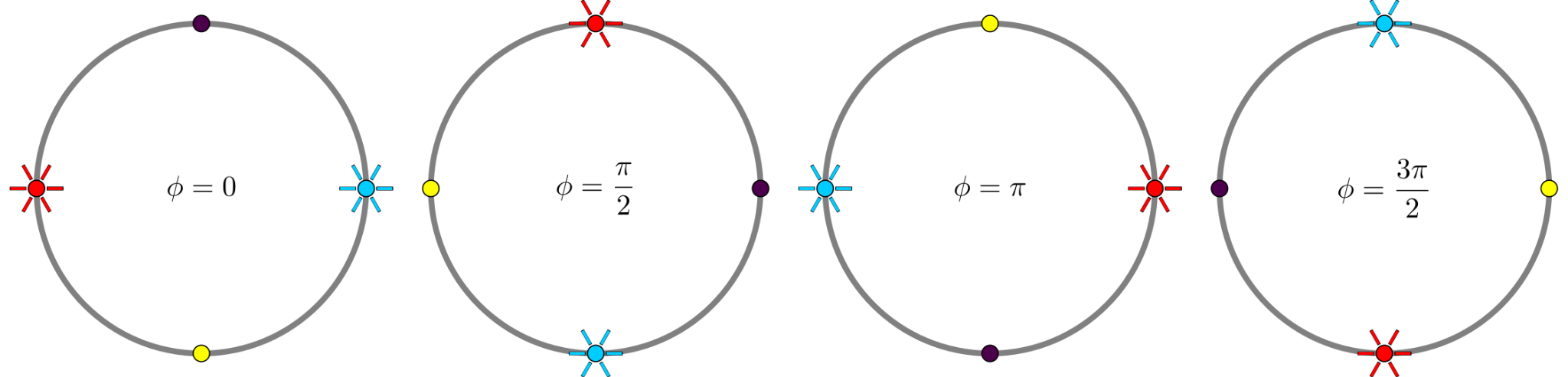
3^o

rotation.in	rotation.out
6 12 0 1 3 6 7 9	2

Εξήγηση: Σε αυτό το παράδειγμα, ο Αζώρ βλέπει έξι διαφορετικές εικόνες που προκύπτουν αντίστοιχα όταν \(\phi \in \{ 0, \pi/6, \pi/3, \pi/2, 2\pi/3, 5\pi/6 \}\).

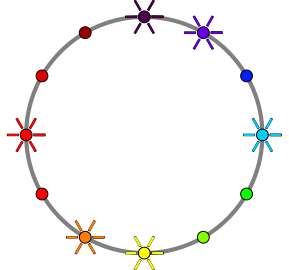
Περιορισμοί:

\(1 \leq N \leq T \leq 10^{18}\),
\(N \leq 10^6\).

Προσέξτε ότι οι τιμές του \(T\), άρα και η τιμή του αποτελέσματος που πρέπει να τυπωθεί, μπορούν να είναι μεγαλύτερες από \(2^{32}\). Επίσης, προσέξτε ότι το μέγεθος των δεδομένων εισόδου μπορεί να είναι μεγάλος. Σας συστήνουμε να διαβάσετε τα δεδομένα με αποδοτικό τρόπο (βλ. <cstdio> και scanf).

Subtasks

Για περιπτώσεις ελέγχου συνολικής αξίας 10%, θα είναι \(T \leq 10^3\).
Για περιπτώσεις ελέγχου συνολικής αξίας 30%, θα είναι \(N \leq 16.000\).
Για περιπτώσεις ελέγχου συνολικής αξίας 40%, θα είναι \(T ≤ 10^6\).
Για περιπτώσεις ελέγχου συνολικής αξίας 70%, θα είναι \(T \leq 10^9\).