37ος ΠΔΠ Α' Φάση
Πολύγωνο κουτιών (polybox)
Η προσπάθεια του Τάκη να φτιάξει όμοιες πίτσες απέτυχε παταγωδώς! Για να μπορέσει να ξεχαστεί, ο Τάκης αποφάσισε να παίξει με μερικά κουτιά πίτσας. Συγκεκριμένα, έχει αγοράσει \(N\) κουτιά σε σχήμα ορθογωνίου παραλληλογράμμου. Το \(i\)-οστό κουτί έχει πλάτος \(w_i\) και ύψος \(h_i\).
Αρχικά, ο Τάκης έβαλε το πρώτο κουτί στο πάτωμα, έπειτα έβαλε το δεύτερο κουτί από πάνω του, και ούτω καθεξής, δημιουργώντας έναν πύργο. Τα κουτιά τοποθετήθηκαν με προσανατολισμό τέτοιον ώστε οι πλευρές με μήκος \(w_i\) να είναι παράλληλες προς το έδαφος. Επιπλέον, επειδή ο Τάκης είναι τελειομανής, φρόντισε ο πύργος του να έχει κατακόρυφο άξονα συμμετρίας, όπως φαίνεται στο ακόλουθο σχέδιο.
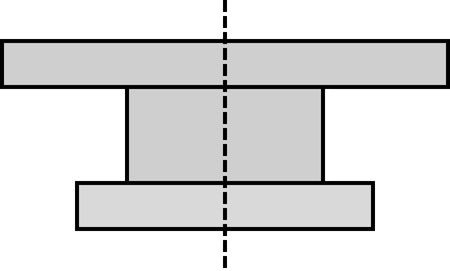
Ο Τάκης σας ζητάει να υπολογίσετε την περίμετρο του σχήματος που δημιουργείται, καθώς όταν προσπάθησε να το κάνει μόνος του ζαλίστηκε από τα πολλά νούμερα.
Πρόβλημα
Να αναπτύξετε ένα πρόγραμμα σε μια από τις γλώσσες του ΠΔΠ (PASCAL, C, C++, Java) το οποίο θα διαβάζει τα δεδομένα εισόδου από το αρχείο polybox.in και θα εκτυπώνει τα αποτελέσματα στο αρχείο polybox.out.
Δεδομένα εισόδου (polybox.in)
Η πρώτη γραμμή περιέχει τον αριθμό του υποπροβλήματος (βλ. παρακάτω). Η δεύτερη γραμμή περιέχει έναν ακέραιο αριθμό \(N\): το πλήθος των κουτιών. Ακολουθούν \(N\) γραμμές, καθεμία από τις οποίες περιέχει δύο ακέραιους αριθμούς \(w_i\) και \(h_i\), χωρισμένους μεταξύ τους με ένα κενό διάστημα: το πλάτος και το ύψος του \(i\)-οστού κουτιού. Τα κουτιά δίνονται με τη σειρά που τοποθετούνται στον πύργο του Τάκη, από κάτω προς τα πάνω.
Δεδομένα εξόδου (polybox.out)
Πρέπει να περιέχει μία μόνο γραμμή με έναν ακέραιο αριθμό: την περίμετρο του σχήματος που δημιουργήθηκε.
Παράδειγμα αρχείων εισόδου-εξόδου
| polybox.in | polybox.out |
|---|---|
| 3 3 6 1 4 2 9 1 |
30 |
Εξήγηση παραδείγματος:
Το παράδειγμα αντιστοιχεί στο παραπάνω σχέδιο. Το κάτω κουτί έχει πλάτος \(6\) και ύψος \(1\), το μεσαίο έχει πλάτος \(4\) και ύψος \(2\) και το επάνω έχει πλάτος \(9\) και ύψος \(1\). Μπορεί κανείς να υπολογίσει, και με την βοήθεια του σχεδίου, ότι η περίμετρος αυτού του σχήματος ισούται με \(30\).
Περιορισμοί
- \(1 \leq N \leq 100.000\),
- \(1 \leq w_i, h_i \leq 10^{40}\).
Υποπροβλήματα
- (5 βαθμοί) \(w_1 = w_2 = \ldots = w_N\) (όλα τα πλάτη είναι ίσα), \(w_i \leq 10^9\) και \(h_i \leq 10^9\)
- (25 βαθμοί) \(N \leq 2\), \(w_i \leq 10^9\) και \(h_i \leq 10^9\)
- (60 βαθμοί) \(w_i \leq 10^9\) και \(h_i \leq 10^9\)
- (10 βαθμοί) Δεν υπάρχουν περαιτέρω περιορισμοί
Παρατηρήσεις:
Μορφοποίηση: Στην είσοδο αλλά και στην έξοδο, κάθε γραμμή τερματίζει με έναν χαρακτήρα newline.
Μέγιστος χρόνος εκτέλεσης: \(2\) sec.
Μέγιστη διαθέσιμη μνήμη: \(128\) MB.