37ος ΠΔΠ Γ' Φάση
Αλυσίδες κριτικών (reviews)
[ Μονάδες]
Οι καλές κριτικές και η διάδοσή τους βοηθούν σημαντικά στην ανάπτυξη της πιτσαρίας του Τάκη, ο οποίος έχει παρατηρήσει ότι η διάδοση των κριτικών είναι μια αλυσιδωτή αντίδραση: μια κριτική διαδίδεται μεταξύ πελατών που έχουν φιλικές σχέσεις.
Για να μελετήσει καλύτερα αυτό το φαινόμενο, ο Τάκης μοίρασε ένα ερωτηματολόγιο σε \(N\) τακτικούς πελάτες του, αριθμημένους από το 1 έως και το \(N\). Καθένας από αυτούς απάντησε αναφέροντας έναν φίλο του. Συγκεκριμένα, ξέρουμε ότι ο \(i\)-οστός πελάτης απάντησε ότι ο πελάτης \(f_i\) είναι φίλος του.
Προφανώς, δεν γίνεται κάποιος πελάτης να έδωσε ως απάντηση τον εαυτό του, άρα σίγουρα \(f_i \neq i\), για κάθε \(i\) (\(1 \leq i \leq N\)). Επίσης, προκειμένου οι απαντήσεις που θα λάμβανε να είχαν κάποια ποικιλία, ο Τάκης δεν επέτρεψε δύο φίλοι να πουν ο καθένας το όνομα του άλλου, δηλαδή δεν υπάρχουν πελάτες \(i\) και \(j\), τέτοιοι ώστε \(f_i = j\) και \(f_j = i\). Θεωρούμε ότι οι φιλίες είναι αμφίδρομες σχέσεις, άρα θα λέμε ότι ο \(f_i\) είναι φίλος του \(i\), αλλά και ο \(i\) είναι φίλος του \(f_i\).
Ονομάζουμε “αλυσίδα διάδοσης μήκους \(M\)” (\(M > 1\)) μια ακολουθία πελατών \(p_1, p_2, \ldots , p_M\), όταν για κάθε \(j\), με \(1 \leq j < M\), ισχύει ότι οι πελάτες \(p_j\) και \(p_{j+1}\) είναι φίλοι και κάθε πελάτης εμφανίζεται το πολύ μία φορά στην ακολουθία \(p\).
Θα λέμε ότι για τους \(N\) πελάτες ισχύει η συνθήκη συνδεσιμότητας, αν για κάθε πελάτη \(i\) και κάθε πελάτη \(j\) υπάρχει τουλάχιστον μία αλυσίδα διάδοσης που να περιέχει και τον πελάτη \(i\) και τον πελάτη \(j\) (όχι αναγκαστικά η ίδια αλυσίδα σε όλες τις περιπτώσεις). Ο Τάκης γνωρίζει ότι με βάση τις φιλίες που προκύπτουν από τις απαντήσεις που έλαβε, ισχύει η συνθήκη συνδεσιμότητας.
Βέβαια, στην πόλη του Τάκη, οι φιλίες είναι κάπως ασταθείς. Μια μέρα στα καλά καθούμενα, μπορεί δύο φίλοι να τσακωθούν και να μη μιλούν για το υπόλοιπο της μέρας. Έτσι, για κάθε πελάτη \(i\) ο Τάκης θέλει να ξέρει τα εξής: Αν σταματήσουμε να θεωρούμε φίλους τον \(i\) και τον \(f_i\):
- Εξακολουθεί να ισχύει η συνθήκη συνδεσιμότητας;
- Αν ναι, ποιο είναι το μέγιστο μήκος που μπορεί να έχει μια αλυσίδα διάδοσης σε αυτήν την περίπτωση;
Σημειώνεται ότι τα σενάρια αυτά είναι ανεξάρτητα μεταξύ τους, δηλαδή κάθε φορά θεωρούμε προσωρινά ότι ακριβώς μία φιλία παύει να υπάρχει. Μιας και ο Τάκης ακόμα προσπαθεί να λύσει τις απορίες του για τον κώδικα του παππού του (από το προηγούμενο πρόβλημα), θα πρέπει για άλλη μία φορά να αναλάβετε δράση.
Πρόβλημα
Να αναπτύξετε ένα πρόγραμμα σε μια από τις γλώσσες του ΠΔΠ (PASCAL, C, C++, Java) το οποίο θα διαβάζει τα δεδομένα εισόδου από το αρχείο reviews.in και θα εκτυπώνει τα αποτελέσματα στο αρχείο reviews.out.
Δεδομένα εισόδου (reviews.in):
Η πρώτη γραμμή περιέχει τον αριθμό του υποπροβλήματος (βλ. παρακάτω). Η δεύτερη γραμμή περιέχει έναν ακέραιο αριθμό \(N\): το πλήθος των τακτικών πελατών της πιτσαρίας. Η τρίτη γραμμή αποτελείται από \(N\) ακέραιους αριθμούς \(f_1, f_2, \ldots, f_N\): τις απαντήσεις των πελατών.
Δεδομένα εξόδου (reviews.out):
Πρέπει να αποτελείται από \(N\) γραμμές, καθεμία από τις οποίες να περιέχει ακριβώς έναν ακέραιο αριθμό: \(−1\) αν μετά την (προσωρινή) αφαίρεση της φιλίας \((i, f_i)\) δεν ισχύει η συνθήκη συνδεσιμότητας, αλλιώς το μέγιστο μήκος αλυσίδας διάδοσης που μπορεί να υπάρξει χωρίς την φιλία \((i, f_i)\).
Παραδείγματα εισόδου - εξόδου:
| reviews.in | reviews.out |
|---|---|
| 5 7 3 7 7 1 2 2 1 |
5 -1 5 -1 -1 -1 6 |
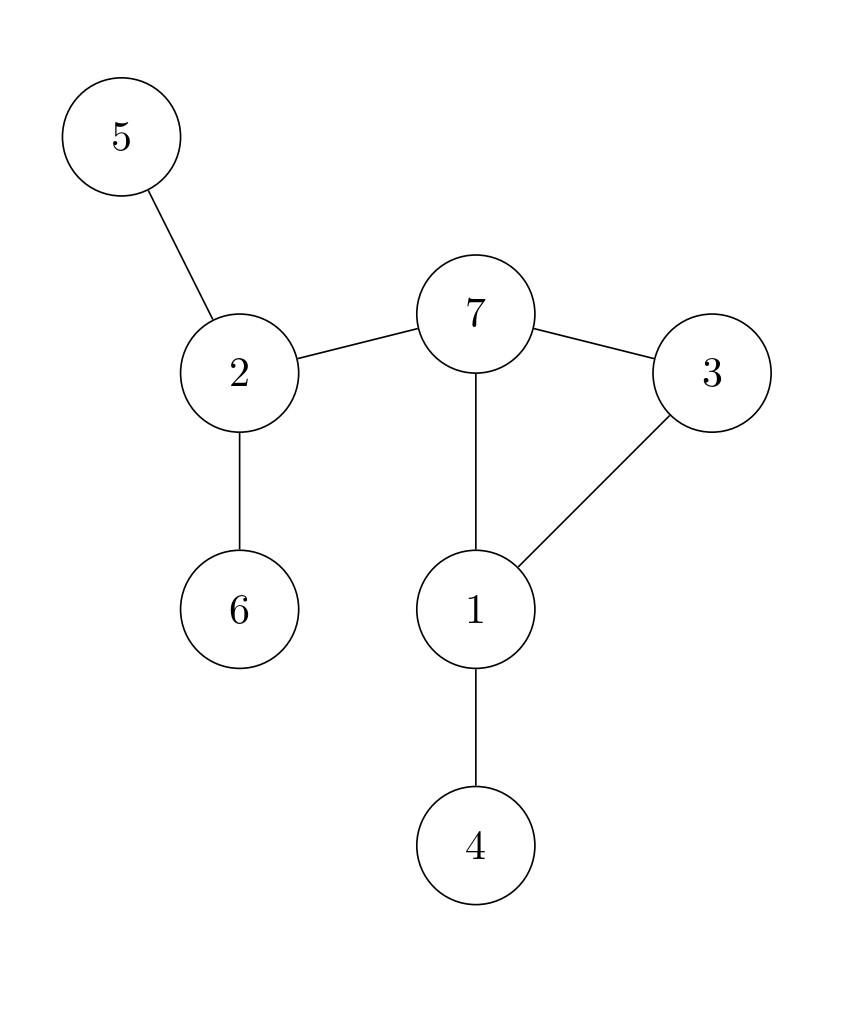
Εξήγηση παραδείγματος: Αν κάποια από τις φιλίες \((2, 7)\), \((4, 1)\), \((5, 2)\) ή \((6, 2)\) σταματήσει να υπάρχει, τότε παρατηρούμε ότι δεν είναι δυνατό να διαδοθεί μια κριτική από οποιονδήποτε πελάτη σε οποιονδήποτε άλλον. Για παράδειγμα, χωρίς την φιλία \((2, 7)\) δεν γίνεται μια κριτική του πελάτη \(1\) να διαδοθεί αλυσιδωτά στον πελάτη \(6\).
Όσον αφορά τις υπόλοιπες φιλίες, με την αφαίρεση μιας από αυτές συνεχίζει να ισχύει η συνθήκη συνδεσιμότητας. Όσον αφορά το μέγιστο μήκος αλυσίδας διάδοσης: για παράδειγμα χωρίς την φιλία \((7, 1)\) μπορεί να υπάρξει αλυσίδα μήκους 6, που είναι και το μέγιστο δυνατό πλήθος, ως εξής: \(4 \to 1 \to 3 \to 7 \to 2 \to 5\).
Περιορισμοί:
- \(3 \leq Ν \leq 200.000\).
- \(1 \leq f_i \leq N\) και \(f_i \neq i\).
- Δεν υπάρχει ζεύγος πελατών \(i\) και \(j\), τέτοιο ώστε \(f_i = j\) και \(f_j = i\).
Υποπροβλήματα:
- (5 βαθμοί) \(f_i = i+1\), για κάθε \(i\) (\(1 \leq i < N\)) και \(f_N = 1\)
- (10 βαθμοί) \(N \leq 250\)
- (18 βαθμοί) Οι φιλίες για τις οποίες δεν προκύπτει απάντηση \(−1\) είναι ακριβώς \(3\).
- (23 βαθμοί) Οι φιλίες για τις οποίες δεν προκύπτει απάντηση \(−1\) είναι το πολύ \(500\).
- (14 βαθμοί) Οι φιλίες για τις οποίες δεν προκύπτει απάντηση \(−1\) είναι το πολύ \(5.000\).
- (30 βαθμοί) Δεν υπάρχουν περαιτέρω περιορισμοί.
Παρατηρήσεις:
Μορφοποίηση: Στην είσοδο αλλά και στην έξοδο, κάθε γραμμή τερματίζει με έναν χαρακτήρα newline.
Μέγιστος χρόνος εκτέλεσης: 1 sec.
Μέγιστη διαθέσιμη μνήμη: 128 MB.