24ος ΠΔΠ Γ' Φάση: Λουτράκι (loutraki) - Λύση
Επεξήγηση εκφώνησης
Μας δίνεται ένας πίνακας με \(N\) σημεία και μας ζητείται να υπολογίσουμε πόσα από τα σημεία δεν κρύβονται ούτε από την αριστερή τους πλευρά αλλά ούτε και από την κάτω τους πλευρά. Για την καλύτερη κατανόηση λόγο της ύπαρξης τόσο θετικών όσο και αρνητικών τιμών στις συντεταγμένες δείτε το παρακάτω σχεδιάγραμμα
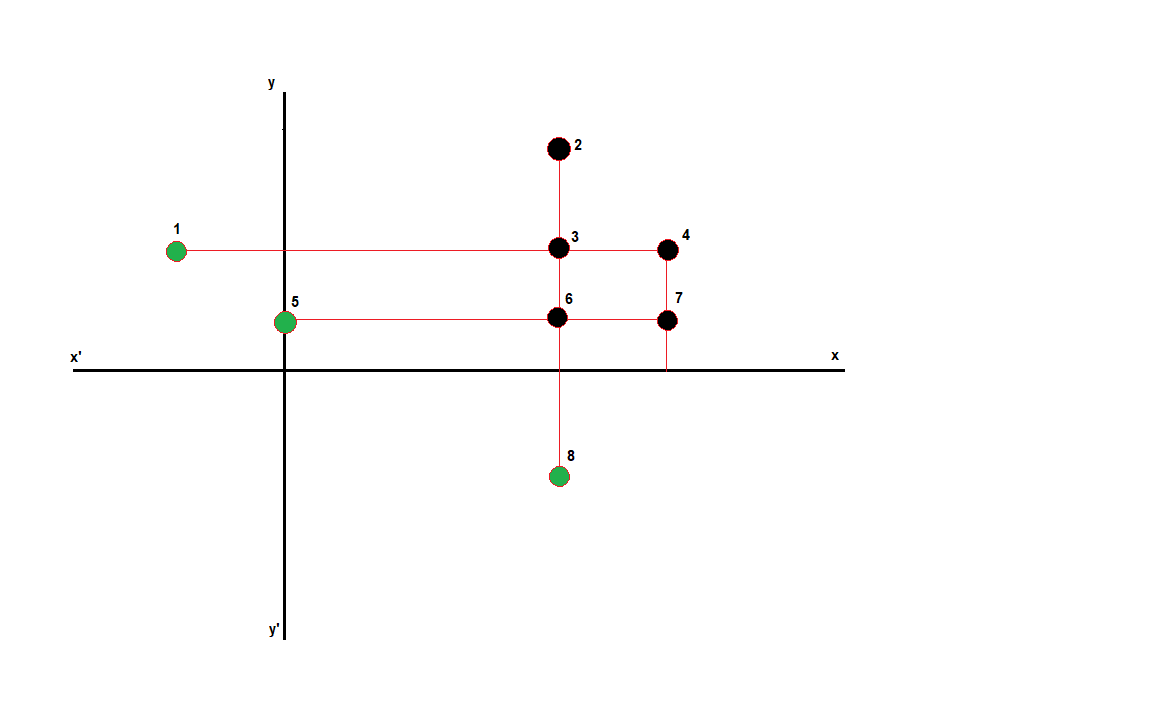
Στο παραπάνω παράδειγμα, μόνο τα πράσινα ξενοδοχεία θεωρούνται προνομιούχα. Πιο αναλυτικά:
Το ξενοδοχείο 1 δεν κρύβεται από κανένα άλλο.
Το ξενοδοχείο 2 κρύβεται από τα 3,6,8.
Το ξενοδοχείο 3 κρύβεται από τα 1,6,8.
Το ξενοδοχείο 4 κρύβεται από τα 3,1,7.
Το ξενοδοχείο 5 δεν κρύβεται από κανένα άλλο.
Το ξενοδοχείο 6 κρύβεται από τα 5 και 8.
Το ξενοδοχείο 7 κρύβεται από τα 5 και 6.
Το ξενοδοχείο 8 δεν κρύβεται από κανένα άλλο.
Αργή λύση \(\mathcal{O}(N^2)\)
Δοκιμάζουμε για κάθε ένα από τα \(N\) ξενοδοχεία όλους τους \(N-1\) συνδυασμούς για να βρούμε αν κρύβεται από κάποιο άλλο. Συνολική πολυπλοκότητα \(\mathcal{O}(N^2)\) .
Παρακάτω δίνεται μία ενδεικτική υλοποίηση αυτής της λύσης.
#include <bits/stdc++.h>
using namespace std;
const long MAXN = long(1e6);
long N, ans;
pair<long,long> hotel[MAXN+1];
#define xx first
#define yy second
int main() {
#ifdef CONTEST
freopen("loutraki.in","r",stdin);
freopen("loutraki.out","w",stdout);
#endif
scanf("%ld", &N);
for(long i=1; i<=N; ++i)
scanf("%ld%ld",&hotel[i].xx,&hotel[i].yy);
for(long i=1;i<=N;++i){
bool hidden = false;
for(long j=1;j<=N && !hidden;j++){
if(i==j)continue;
if(hotel[j].xx == hotel[i].xx && hotel[j].yy < hotel[i].yy)
hidden = true;
if(hotel[j].yy == hotel[i].yy && hotel[j].xx < hotel[i].xx)
hidden = true;
}
if(!hidden)
ans++;
}
printf("%ld\n", ans);
return 0;
}
Mέτρια λύση - \(\mathcal{O}(N \cdot log(N))\) - line sweep
Γνώσεις που θα χρειαστούμε: lambda functions (c++11 και νεότερες)
Ταξινομούμε τα ξενοδοχεία πρώτα ως προς \(x\) και μετά ως προς \(y\) στον πίνακα \(C[]\). Σαρώνουμε από τις μικρότερες προς τις μεγαλύτερες ώστε να ενημερώσουμε τον πίνακα των ξενοδοχείων για το αν έχουν ορατότητα από αυτή την πλευρά. Αξιοποιούμε το πρώτο στοιχείο που συναντούμε και πετάμε τα υπόλοιπα με την ίδια τιμή στη συντεταγμένη \(x\). Το ίδιο θα κάνουμε και για το \(y\).
Η ταξινόμηση γίνεται με χρήση δικών μας συναρτήσεων σύγκρισης. Προτιμήθηκε η λύση της lambda (inline σύντομες συναρτήσεις) για να δειχθεί αυτή η λειτουργία της c++.
sort(C+1,C+N+1,[](const auto& a,const auto& b){return (a.x==b.x)?(a.y<b.y):(a.x<b.x);});
Στην παραπάνω εντολή ταξινομούμε τον πίνακα \(C[]\) πρώτα με το \(x\) και σε περίπτωση ισότητας με το \(y\). Η συνάρτηση:
[](const auto& a,const auto& b){return (a.x==b.x)?(a.y<b.y):(a.x<b.x);}
λέγεται lambda συνάρτηση και είναι η συνάρτηση σύγκρισης που θα χρησιμοποιήσει η sort. Μέσα στα άγκιστρα αυτό που κάνει είναι απλά να συγκρίνει τις συντεταγμένες δυο αντικειμένων του πίνακα, των \(a\) και \(b\). Μέσα στις \([]\) πρέπει να δηλώσουμε αν και πως η lambda μας θα έχει πρόσβαση σε άλλες μεταβλητές του προγράμματος εκτός από αυτές που παίρνει ως παραμέτρους. Η συγκεκριμένη lambda δεν χρειάζεται τίποτα άλλο από τα δυο στοιχεία του πίνακα οπότε παραμένει κενό το τμήμα αυτό.
Η λύση αυτή περνά τα 12 από τα 15 test cases.
#include <bits/stdc++.h>
using namespace std;
const long MAXN = long(1e6);
const long OFFSET = long(1e5);
struct hotel {
long x,y,visibility;
hotel(long x,long y): x(x), y(y) { visibility = 0; }
hotel(){ x = y = visibility = 0; }
} hotel[MAXN+1];
struct coord {
long x,y,hotel_id;
coord(long x,long y,long hotel_id):x(x),y(y),hotel_id(hotel_id){}
coord(){ x = y = hotel_id = 0; }
} C[MAXN+1];
long N, ans;
int main() {
#ifdef CONTEST
freopen("loutraki.in","r",stdin);
freopen("loutraki.out","w",stdout);
#endif
scanf("%ld", &N);
for(long i=1; i<=N; ++i){
scanf("%ld%ld",&hotel[i].x,&hotel[i].y);
hotel[i].x += OFFSET;
hotel[i].y += OFFSET;
C[i] = coord( hotel[i].x, hotel[i].y, i );
}
sort(C+1,C+N+1,[](const auto& a,const auto& b){return (a.x==b.x)?(a.y<b.y):(a.x<b.x);});
for(long i=1;i<=N;){
long co = C[i].x;
hotel[C[i].hotel_id].visibility++;
while(i<=N && C[i].x == co)
i++;
}
sort(C+1,C+N+1,[](const auto& a,const auto& b){return (a.y==b.y)?(a.x<b.x):(a.y<b.y);});
for(long i=1;i<=N;){
long co = C[i].y;
//hotel[C[i].hotel_id].visibility++;
if(++hotel[C[i].hotel_id].visibility == 2)
ans++;
while(i<=N && C[i].y == co)
i++;
}
printf("%ld\n", ans);
return 0;
}
Μέτρια λύση - \(\mathcal{O}(N \cdot log(N))\)
Γνώσεις που θα χρειαστούμε: std::vector, std::sort (C++ stl)
Η λύση που θα δούμε εισάγει ιδέες που θα χρειαστούν για την βέλτιστη λύση.
Αποθηκεύουμε για κάθε διακριτή συντεταγμένη όλες τις αντίστοιχες συντεταγμένες του άλλου άξονα. Θα ελέγξουμε το κάθε ένα από τα \(N\) ξενοδοχεία, αν επικαλύπτεται από κάποιο άλλο σε πολυπλοκότητα \(\mathcal{O}(logN)\).
Η λύση αυτή περνά τα 12 από τα 15 test cases.
Μία ενδεικτική υλοποίηση παρουσιάζεται παρακάτω:
#include <bits/stdc++.h>
using namespace std;
const long MAXN = long(1e6);
const long OFFSET = long(1e5);
vector<long> X[2*OFFSET+1],Y[2*OFFSET+1];
long N, ans;
pair<long,long> hotel[MAXN+1];
#define xx first
#define yy second
int main() {
#ifdef CONTEST
freopen("loutraki.in","r",stdin);
freopen("loutraki.out","w",stdout);
#endif
scanf("%ld", &N);
for(long i=1; i<=N; ++i){
scanf("%ld%ld",&hotel[i].xx,&hotel[i].yy);
hotel[i].xx+=OFFSET;
hotel[i].yy+=OFFSET;
X[hotel[i].xx].push_back(hotel[i].yy);
Y[hotel[i].yy].push_back(hotel[i].xx);
}
for(long x=0;x<2*OFFSET;x++)sort(X[x].begin(),X[x].end());
for(long y=0;y<2*OFFSET;y++)sort(Y[y].begin(),Y[y].end());
for(long i=1;i<=N;++i){
if(X[hotel[i].xx][0] == hotel[i].yy && Y[hotel[i].yy][0] == hotel[i].xx)
ans++;
//αν η μικρότερη τιμή είναι η δικιά μας και στις δύο συντεταγμένες,
//τότε είμαστε προνομοιούχοι
}
printf("%ld\n", ans);
return 0;
}
Παρατήρηση
Σε κάθε διακριτή τιμή τετμημένης(\(x\)) ή τεταγμένης(\(y\)) μας ενδιαφέρει μόνο το ξενοδοχείο με την μικρότερη τεταγμένη ή τετμημένη αντίστοιχα γι’ αυτό και στην προηγούμενη λύση χρησιμοποιούσαμε μόνο το πρώτο στοιχείο του vector. Δηλαδή από όλα τα ξενοδοχεία με ίδιο \(x\) μας ενδιαφέρει μόνο το ξενοδοχείο με το μικρότερο \(y\). Οπότε είμαστε έτοιμοι για την λύση με γραμμική πολυπλοκότητα που ακολουθεί.
Βέλτιστη λύση - \(\mathcal{O}(N)\)
Επεξεργαζόμαστε κάθε ξενοδοχείό με τη σειρά που το διαβάζουμε από το αρχείο. Το υπο εξέταση ξενοδοχείο θα το ελέγξουμε ξεχωριστά για την κάθε συντεταγμένη.
Κρατάμε στη θέση \(X[x]\) του πίνακα \(X[]\) τον αριθμό του ξενοδοχείου \((x,y)\) με τη μικρότερη τεταγμένη \(y\). Αντίστοιχα κρατάμε και στη θέση \(Y[y]\) του πίνακα \(Y[]\) τον αριθμό του ξενοδοχείου \((x,y)\) με τη μικρότερη τετμημένη \(x\).
Αν δεν υπάρχει κανένα ξενοδοχείο με το ίδιο \(x\) τότε δεν το κρύβει κανένα άλλο από το να “βλέπει” προς τα κάτω οπότε αυτό αποκτά ορατότητα από την πλευρά αυτή. Αν υπάρχει ξενοδοχείο με το ίδιο \(x\) τότε υπάρχουν δυο περιπτώσεις, ή το υπο εξέταση ξενοδοχείο κρύβεται από το ξενοδοχείο \(X[x]\) ή θα κρύψει το παλιότερο ξενοδοχείο \(X[x]\).
Στην περίπτωση που κρυφτεί το παλιό ξενοδοχείο πρέπει να δώσουμε προσοχή στο αν πρέπει να διορθώσουμε την μεταβλητή \(\mathit{ans}\). Αν το παλιό ξενοδοχείο είχε επηρεάσει την μεταβλητή \(\mathit{ans}\) τότε πρέπει να την μειώσουμε, πράγμα που κάνει το παρακάτω απόσπασμα κώδικα:
void hide_hotel(long i){//hide a previously processed hotel.
if(!hidden[i]){
ans--;//i is no more part of answer
hidden[i] = true;
}
}
Μια σημείωση: θα μπορούσαμε να μην κάνουμε διορθώσεις στη μεταβλητή \(\mathit{ans}\) καθώς επεξεργαζόμαστε τα ξενοδοχεία και απλά στο τέλος του προγράμματος να κάνουμε ένα βρόγχο επανάληψης και να καταμετρήσουμε πόσα flags είναι σβηστά στον πίνακα \(\mathit{hidden[]}\) και να τυπώσουμε αυτόν τον αριθμό.
Αφού κάνουμε τον ίδιο έλεγχο και για την τεταγμένη \(y\) έχουμε μετρήσει από πόσες πλευρές έχει ορατότητα το ξενοδοχείο μας. Αν είναι \(visibility == 2\) τότε το ξενοδοχείο μας είναι προνομιούχο τουλάχιστο μέχρι αυτή τη στιγμή.
Πολυπλοκότητα: Η εξέταση κάθε ξενοδοχείου γίνεται μόνο μια φορά και ο υπολογισμός αν κρύβεται ή κρύβει γίνεται σε \(\mathcal{O}(1)\) άρα η συνολική μας πολυπλοκότητα είναι \(\mathcal{O}(N)\).
Μία ενδεικτική υλοποίηση παρουσιάζεται παρακάτω:
#include <bits/stdc++.h>
using namespace std;
const long MAXN = long(1e6);
const long OFFSET = long(1e5);
bool hidden[MAXN+5]; //true if hotel i is blocked
long X[2*OFFSET+2],Y[2*OFFSET+5];//what is the frontmost id of the hotel in this axis
pair<long,long> hotel[MAXN+5];
long N, ans;
#define xx first
#define yy second
void hide_hotel(long i){//hide a previously processed hotel.
if(!hidden[i]){
ans--;//i is no more part of answer
hidden[i] = true;
}
}
int main() {
#ifdef CONTEST
freopen("loutraki.in","r",stdin);
freopen("loutraki.out","w",stdout);
#endif
scanf("%ld", &N);
for(long x,y,i=1; i<=N; ++i){
scanf("%ld%ld",&x,&y);
x+=OFFSET; y+=OFFSET; //make positive
hotel[i] = {x,y};
long visibility = 0;
//will we hide some other hotel from viewing xx' axis?
if(X[x]){//there is a hotel with same x
if(y < hotel[X[x]].yy){ //yes, replace old one X[x]
hide_hotel(X[x]);
X[x] = i;
visibility++;
}
} else {//first hotel in that x pos
X[x] = i;
visibility++;
}
//will we hide some other hotel from viewing yy' axis?
if(Y[y]){//there is a hotel with same y
if(x < hotel[Y[y]].xx){//yes, replace old one Y[y]
hide_hotel(Y[y]);
Y[y] = i;
visibility++;
}
} else {//first hotel in that y pos
Y[y] = i;
visibility++;
}
if(visibility<2)
hidden[i] = true;
else
ans++;
}
printf("%ld\n", ans);
return 0;
}
Γενική Παρατήρηση στις διαστάσεις των πινάκων
Στον πίνακα \(\mathit{hotel[ ]}\) χρησιμοποιούμε τα στοιχεία \(1\) έως και \(N\) άρα πρέπει να έχει μέγεθος \(10^6+1\).
Στους πίνακες \(X[ ]\) και \(Y[ ]\) θέλουμε να αποθηκεύουμε τιμές από \(-10^5\) έως και \(+10^5\) οι οποίες είναι \(10^5\) από κάθε κατεύθυνση του άξονα συντεταγμένων και μια ακόμα τιμή που είναι το \(0\) οπότε \(2\cdot 10^5 + 1\) τιμές συνολικά.
Λόγω του ότι είναι εύκολο να γίνει λάθος που θα παράγει σφάλμα κατάτμησης (segmentation fault) είναι προτιμότερο στους διαγωνισμούς να δεσμεύονται μερικά στοιχεία περισσότερο στους πίνακες (π.χ. 5 στοιχεία παραπάνω από ότι υπολογίζουμε ότι χρειάζεται) και ας μην χρησιμοποιηθούν, παρά να χαθούν test cases από τέτοιες λεπτομέρειες.
const long MAXN = long(1e6);
const long OFFSET = long(1e5);
bool hidden[MAXN+5]; //true if hotel i is blocked
long X[2*OFFSET+2],Y[2*OFFSET+5];//what is the frontmost id of the hotel in this axis
pair<long,long> hotel[MAXN+5];